Question

【题目】如图是抛物线y=ax2+bx+c（a≠0），其顶点为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间，则下列结论正确的是（ ）

①若抛物线与x轴的另一个交点为（k，0），则－2＜k＜－1； ②c－a=n；

③若x＜－m时，y随x的增大而增大，则m=－1；④若x＜0时，ax2+（b+2）x＜0.

A. ①②④ B. ①③④ C. ①② D. ①②③④

Answer 1

【答案】A

【解析】根据抛物线的顶点和与x轴的交点，其对称轴为x=-=1，则b=-2a，可由抛物线与x轴的另一个交点为（k，0），则或，解得k=-1或k=-2，即－2＜k＜－1，故①正确；当x=1时，n=a+b+c，即a-2a+c=n，即c-a=n，故②正确；根据二次函数的增减性，可知当x＜1时，y随x增大而增大，可知m＜-1，故③不正确；由抛物线的开口向下，则a＜0，所以y=ax2+（b+2）x也开口向下，且过原点，因此当y=0时，ax2+（b+2）x=0，因式分解为x（ax+b+2）=0，所以x=0或x=，所以y =ax2+（b+2）x=＞0，如图，

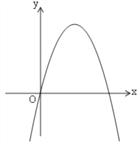
所以当x＜0时，y=ax2+（b+2）x＜0，故④正确.

故选：A.