
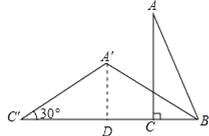
【题目】如图,书桌上的一种新型台历和一块主板AB、一个架板AC和环扣(不计宽度,记为点A)组成,其侧面示意图为△ABC,测得AC⊥BC,AB=5cm,AC=4cm,现为了书写记事方便,须调整台历的摆放,移动点C至C′,当∠C′=30°时,求移动的距离即CC′的长(或用计算器计算,结果取整数,其中![]() =1.732,
=1.732, ![]() =4.583)
=4.583)

【答案】5cm
【解析】试题分析:过点A′作A′D⊥BC′,垂足为D,先在△ABC中,由勾股定理求出BC=3cm,再解Rt△A′DC′,得出A′D=2cm,C′D=2![]() cm,在Rt△A′DB中,由勾股定理求出BD=
cm,在Rt△A′DB中,由勾股定理求出BD=![]() cm,然后根据CC′=C′D+BD﹣BC,将数据代入,即可求出CC′的长.
cm,然后根据CC′=C′D+BD﹣BC,将数据代入,即可求出CC′的长.
试题解析:过点A′作A′D⊥BC′,垂足为D.
在△ABC中,∵AC⊥BC,AB=5cm,AC=4cm,∴BC=3cm.
当动点C移动至C′时,A′C′=AC=4cm.在△A′DC′中,∵∠C′=30°,∠A′DC′=90°,
∴A′D=![]() A′C′=2cm,C′D=
A′C′=2cm,C′D=![]() A′D=2
A′D=2![]() cm.
cm.
在△A′DB中,∵∠A′DB=90°,A′B=5cm,A′D=2cm,∴BD=![]() =
=![]() cm,
cm,
∴CC′=C′D+BD﹣BC=2![]() +
+![]() ﹣3,∵
﹣3,∵![]() =1.732,
=1.732,![]() =4.583,∴CC′=2×1.732+4.583﹣3≈5.
=4.583,∴CC′=2×1.732+4.583﹣3≈5.
故移动的距离即CC′的长约为5cm.


科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=![]() ,BC=
,BC=![]() .某课题小组利用这张矩形纸片依次进行如下操作(每次折叠后均展开).
.某课题小组利用这张矩形纸片依次进行如下操作(每次折叠后均展开).
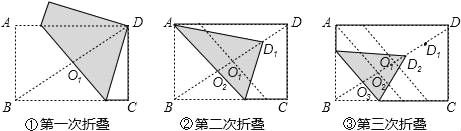
如图①,第一次将纸片折叠,使点B与点D重合,折痕与BD交与点O1,设O1D的中点为D1;
如图②,第二次将纸片折叠,使点B与点D1重合,折痕与BD交与点O2,设O2D3的中点为D2;
如图③,第三次将纸片折叠,使点B与点D2重合,折痕与BD交与点O3,设O3D2的中点为D3;
…
根据以上操作结果,回答下列问题:
(1)如图①,MN是折痕,求证:△DA′M≌△DCN;
(2)分别求出线段BO1、BO2、BO3的长,并直接写出第n次折叠后BOn的长(用含n的式子表示);
(3)如图②,第二次折叠时,折痕一定会经过点A吗?请通过计算判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
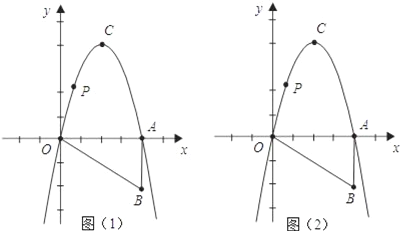
【题目】如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB绕点O逆时针旋转90°,点B旋转到点C的位置,一条抛物线正好经过点O,C,A三点.
(1)求该抛物线的解析式;
(2)在x轴上方的抛物线上有一动点P,过点P作x轴的平行线交抛物线于点M,分别过点P,点M作x轴的垂线,交x轴于E,F两点,问:四边形PEFM的周长是否有最大值?如果有,请求出最值,并写出解答过程;如果没有,请说明理由.
(3)如果x轴上有一动点H,在抛物线上是否存在点N,使O(原点)、C、H、N四点构成以OC为一边的平行四边形?若存在,求出N点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在解一元二次方程时,他是这样做的:
解一元二次方程
3x2﹣8x(x﹣2)=0…第一步
3x﹣8x﹣2=0…第二步
﹣5x﹣2=0…第三步
﹣5x=2…第四步
x=﹣![]() …第五步
…第五步
(1)小明的解法从第 步开始出现错误;此题的正确结果是 .
(2)用因式分解法解方程:x(2x﹣1)=3(2x﹣1).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com