练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

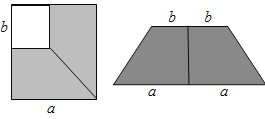
    【题目】如图所示，在边长为a的正方形中减去一个边长为b的小正方形（a＞b），把剩下的部分拼成一个梯形如图，分别计算这两个图阴影部分的面积，验证了公式：_____用此公式计算：_____

    【答案】a2b2=(a+b)(ab) 6x

    【解析】

    根据左图中阴影部分的面积=大正方形的面积-小正方形的面积，或者右图中阴影部分的面积=梯形的面积，由面积不变可得公式．

    左图中阴影部分的面积=a2b2，右图中阴影部分的面积=×(2a+2b)(ab)=(a+b)(ab),由图中阴影部分的面积不变，得a2b2=(a+b)(ab).因此验证的公式为为：a2b2=(a+b)(ab).根据公式计算（）=6x，即答案是a2b2=(a+b)(ab)；6x

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读材料：数学课上，老师展示了一位同学的作业如下：

    已知多项式，，

    （1）求；

    （2）若的结果与字母的取值无关，求的值.

    下面是这位同学第（1）问的解题过程：

    解：（1） …………………………第一步

    …………………………………………………第二步

    ……………………………………………………………第三步

    回答问题：

    （i）这位同学第______步开始出现错误，错误原因是____________；

    （ii）请你帮这位同学完成题目中的第（2）问.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，E是ABCD的边CD的中点，延长AE交BC的延长线于点F．

    （1）求证：△ADE≌△FCE．

    （2）若∠BAF=90°，BC=5，EF=3，求CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＞AC，点D、E分别是边AB、AC的中点，点F在BC边上，连接DE、DF、EF，则添加下列哪一个条件后，仍无法判断△FCE与△EDF全等（ ）

    A. ∠A=∠DFE B. BF=CF C. DF∥AC D. ∠C=∠EDF

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（8分）为了贯彻落实市委市府提出的“精准扶贫”精神．某校特制定了一系列关于帮扶A、B两贫困村的计划．现决定从某地运送152箱鱼苗到A、B两村养殖，若用大小货车共15辆，则恰好能一次性运完这批鱼苗，已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆，其运往A、B两村的运费如下表：

    （1）求这15辆车中大小货车各多少辆？

    （2）现安排其中10辆货车前往A村，其余货车前往B村，设前往A村的大货车为x辆，前往A、B两村总费用为y元，试求出y与x的函数解析式．

    （3）在（2）的条件下，若运往A村的鱼苗不少于100箱，请你写出使总费用最少的货车调配方案，并求出最少费用．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠C=90°，AC=BC，斜边AB=4，O是AB的中点，以O为圆心，线段OC的长为半径画圆心角为90°的扇形OEF， 经过点C，则图中阴影部分的面积为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

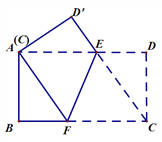
    【题目】如图，将矩形ABCD折叠，使C点与A点重合，折痕为EF.

    （1）判断四边形AFCE的形状，并说明理由；

    （2）若AB=4，BC=8，求折痕EF的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

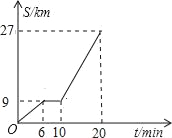
    【题目】如图所示是鼎龙高速路口开往宁都方向的某汽车行驶的路程s（km）与时间t（分钟）的函数关系图，观察图中所提供的信息，解答下列问题：

    （1）汽车在前6分钟内的平均速度是　 　千米/小时，汽车在兴国服务区停了多长时间？　 　分钟；

    （2）当10≤t≤20时，求S与t的函数关系式；

    （3）规定：高速公路时速超过120千米/小时为超速行驶，试判断当10≤t≤20时，该汽车是否超速，说明理由．

    查看答案和解析>>

    同步练习册答案