
科目:初中数学 来源: 题型:解答题
 一拱形隧道的轮廓是抛物线如图,拱高6m,跨度20m,
一拱形隧道的轮廓是抛物线如图,拱高6m,跨度20m,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
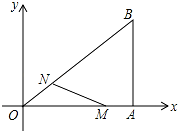 如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
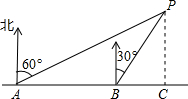 如图,小明同学在东西方向的环海路A处,测得海中灯塔P在它的北偏东60°方向上,在A的正东200米的B处,测得海中灯塔P在它的北偏东30°方向上.问:灯塔P到环海路的距离PC约等于多少米?($\sqrt{3}$取1.732,结果精确到1米)
如图,小明同学在东西方向的环海路A处,测得海中灯塔P在它的北偏东60°方向上,在A的正东200米的B处,测得海中灯塔P在它的北偏东30°方向上.问:灯塔P到环海路的距离PC约等于多少米?($\sqrt{3}$取1.732,结果精确到1米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com