
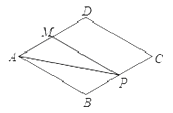
【题目】如图,菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,点P由点A出发,沿A→B→C→D作匀速运动,到达点D停止,则△APM的面积y与点P经过的路程x之间的函数关系的图象大致是( )
A. 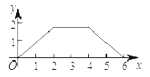 B.
B. 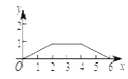 C.
C. 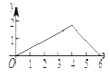 D.
D. 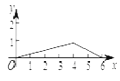
【答案】B
【解析】
分类讨论:当0≤x≤2,如图1,作PH⊥AD于H,AP=x,根据菱形的性质得∠A=60°,AM=1,则∠APH=30°,根据含30度的直角三角形三边的关系得到在RtAH=![]() x,PH=
x,PH=![]() x,然后根据三角形面积公式得y=
x,然后根据三角形面积公式得y=![]() AMPH=
AMPH=![]() x;当2<x≤4,如图2,作BE⊥AD于E,AP+BP=x,根据菱形的性质得∠A=60°,AM=1,AB=2,BC∥AD,则∠ABE=30°,在Rt△ABE中,根据含30度的直角三角形三边的关系得AE=1,PH=
x;当2<x≤4,如图2,作BE⊥AD于E,AP+BP=x,根据菱形的性质得∠A=60°,AM=1,AB=2,BC∥AD,则∠ABE=30°,在Rt△ABE中,根据含30度的直角三角形三边的关系得AE=1,PH=![]() ,然后根据三角形面积公式得y=
,然后根据三角形面积公式得y=![]() AMBE=
AMBE=![]() ;
;
当4<x≤6,如图3,作PF⊥AD于F,AB+BC+PC=x,则PD=6-x,根据菱形的性质得∠ADC=120°,则∠DPF=30°,在Rt△DPF中,根据含30度的直角三角形三边的关系得DF=![]() (6-x),PF=
(6-x),PF=![]() DF=
DF=![]() (6-x),则利用三角形面积公式得y=
(6-x),则利用三角形面积公式得y=![]() AMPF=-
AMPF=-![]() x+
x+![]() ,最后根据三个解析式和对应的取值范围对各选项进行判断.
,最后根据三个解析式和对应的取值范围对各选项进行判断.
当点P在AB上运动时,即0≤x≤2,如图1,

作PH⊥AD于H,AP=x,
∵菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,
∴∠A=60°,AM=1,
∴∠APH=30°,
在Rt△APH中,AH=![]() AP=
AP=![]() x,
x,
PH=![]() AH=
AH=![]() x,
x,
∴y=![]() AMPH=
AMPH=![]() ×1×
×1×![]() x=
x=![]() x;
x;
当点P在BC上运动时,即2<x≤4,如图2,
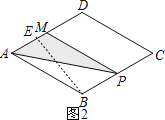
作BE⊥AD于E,AP+BP=x,
∵四边形ABCD为菱形,∠B=120°,
∴∠A=60°,AM=1,AB=2,BC∥AD,
∴∠ABE=30°,
在Rt△ABE中,AE=![]() AB=1,
AB=1,
PH=![]() AE=
AE=![]() ,
,
∴y=![]() AMBE=
AMBE=![]() ×1×
×1×![]() =
=![]() ;
;
当点P在CD上运动时,即4<x≤6,如图3,

作PF⊥AD于F,AB+BC+PC=x,则PD=6-x,
∵菱形ABCD中,∠B=120°,
∴∠ADC=120°,
∴∠DPF=30°,
在Rt△DPF中,DF=![]() DP=
DP=![]() (6-x),
(6-x),
PF=![]() DF=
DF=![]() (6-x),
(6-x),
∴y=![]() AMPF=
AMPF=![]() ×1×
×1×![]() (6-x)=
(6-x)=![]() (6-x)=-
(6-x)=-![]() x+
x+![]() ,
,
∴△APM的面积y与点P经过的路程x之间的函数关系的图象为三段:当0≤x≤2,图象为线段,满足解析式y=![]() x;当2≤x≤4,图象为平行于x轴的线段,且到x轴的距离为
x;当2≤x≤4,图象为平行于x轴的线段,且到x轴的距离为![]() ;当4≤x≤6,图象为线段,且满足解析式y=-
;当4≤x≤6,图象为线段,且满足解析式y=-![]() x+
x+![]() .
.
故选B.


科目:初中数学 来源: 题型:
【题目】如图1,一条细绳系着一个小球在平面内摆动,已知细绳从悬挂点O到球心的长度为50厘米,小球在带你B位置时达到最低点,当小球在左侧点A时与最低点B时细绳相应所成的角度∠AOB=37°.(取sin37°=0.6,cos37°=0.8,tan37°=0.75) 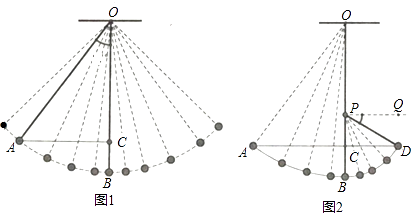
(1)求点A与点B的高度差BC的值.
(2)如图2,若在点O的正下方有一个阻碍物P,当小球从左往右落到最低处后,运动轨迹改变,变为以P为圆心,PB为半径继续向右摆动,当摆动至与点A在同一水平高度的点D时,满足PD部分细绳与水平线的夹角∠DPQ=30°,求OP的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50cm,第2节套管长46cm,以此类推,每一节套管均比前一节套管少4cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为xcm.

(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一圆柱,其高为12cm,它的底面半径为3cm,在圆柱下底面A处有一只蚂蚁,它想得到上面B处的食物,则蚂蚁经过的最短距离为_________.(π取3)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015随州)甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:
①出发1小时时,甲、乙在途中相遇;
②出发1.5小时时,乙比甲多行驶了60千米;
③出发3小时时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数是( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,水平面上有一个坡度i=1:2的斜坡AB,矩形货柜DEFG放置在斜坡上,己知DE=2.5m.EF=2m,BF=3.5m,则点D离地面的高DH为 m.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )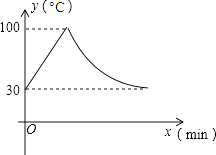
A.7:20
B.7:30
C.7:45
D.7:50
查看答案和解析>>
科目:初中数学 来源: 题型:
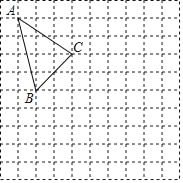
【题目】如图,在正方形网格中,每个小正方形的边长为1,格点△ABC(顶点在网格线的交点上)的顶点A、C的坐标分别为A(﹣3,4)C(0,2)
(1)请在网格所在的平面内建立平面直角坐标系,并写出点B的坐标;
(2)画出△ABC关于原点对称的图形△A1B1C1;
(3)求△ABC的面积;
(4)在x轴上存在一点P,使PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( ) 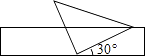
A.3cm
B.6cm
C.![]() cm
cm
D.![]() cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com