
【题目】已知直线y= ![]() x+b与双曲线y=
x+b与双曲线y= ![]() 的一个交点为(2,5),直线与y轴交于点A.
的一个交点为(2,5),直线与y轴交于点A. 
(1)求m的值及点A的坐标;
(2)若点P在双曲线y= ![]() 的图象上,且S△POA=10,求点P的坐标.
的图象上,且S△POA=10,求点P的坐标.
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,经过点A1(1,0)作x轴的垂线与直线l:y= ![]() x相交于点B1 , 以O为圆心,OB1为半径画弧与x轴相交于点A2;经过点A2作x轴的垂线与直线l相交于点B2 , 以O为圆心、OB2为半径画弧与x轴相交于点A3;…依此类推,点A5的坐标是( )
x相交于点B1 , 以O为圆心,OB1为半径画弧与x轴相交于点A2;经过点A2作x轴的垂线与直线l相交于点B2 , 以O为圆心、OB2为半径画弧与x轴相交于点A3;…依此类推,点A5的坐标是( )
A.(8,0)
B.(12,0)
C.(16,0)
D.(32,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB外的一点,点Q是点P关于OA的对称点,点R是点P关于OB的对称点,直线QR分别交∠AOB两边OA,OB于点M,N,连结PM,PN,如果∠PMO=33°,∠PNO=70°,求∠QPN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,AB=2,现将一块三角板的直角顶点放在AB的中点D处,两直角边分别与直线AC,直线BC相交于点E,F,我们把DE⊥AC时的位置定为起始位置(如图1),将三角板绕点D顺时针方向旋转一个角度α(0°<α<90°).
(1)如图2,在旋转过程中,当点E在线段AC上时,试判别△DEF的形状,并说明理由;
(2)设直线ED交直线BC于点G,在旋转过程中,是否存在点G,使得△EFG为等腰三角形?若存在,求出CG的长,若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级(1)班的宣传委员在办黑板报时,采用了下面的图案作为边框,其中每个黑色六边形与6个白色六边形相邻.若一段边框上有45个黑色六边形,则这段边框共有白色六边形( )

A. 182个 B. 180个 C. 272个 D. 270个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
(3)在(2)的条件下,根据市场调查,每套乙种套房的提升费用不会改变,每套甲种套房提升费用将会提高a万元(a>0),市政府如何确定方案才能使费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D. 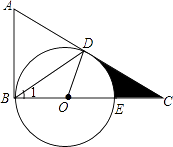
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知y=﹣x+m(m>4)过动点A(m,0),并与反比例函数y= ![]() 的图象交于B、C两点(点B在点C的左边),以OA为直径作反比例函数y=
的图象交于B、C两点(点B在点C的左边),以OA为直径作反比例函数y= ![]() 的图象相交的半圆,圆心为P,过点B作x轴的垂线,垂足为E,并于半圆P交于点D.
的图象相交的半圆,圆心为P,过点B作x轴的垂线,垂足为E,并于半圆P交于点D. 
(1)当m=5时,求B、C两点的坐标.
(2)求证:无论m取何值,线段DE的长始终为定值.
(3)记点C关于直线DE的对称点为C′,当四边形CDC′E为菱形时,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com