
【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
(3)在(2)的条件下,根据市场调查,每套乙种套房的提升费用不会改变,每套甲种套房提升费用将会提高a万元(a>0),市政府如何确定方案才能使费用最少?
【答案】
(1)解:设甲种套房每套提升费用为x万元,依题意,
得 ![]() 解得:x=25
解得:x=25
经检验:x=25符合题意,x+3=28
答:甲,乙两种套房每套提升费用分别为25万元,28万元
(2)解:设甲种套房提升m套,那么乙种套房提升(80﹣m)套,依题意,得
![]()
解得:48≤m≤50
即m=48或49或50,所以有三种方案分别是:
方案一:甲种套房提升48套,乙种套房提升32套.
方案二:甲种套房提升49套,乙种套房提升31套,
方案三:甲种套房提升50套,乙种套房提升30套.
设提升两种套房所需要的费用为W万元.则
W=25m+28×(80﹣m)=﹣3m+2240,
∵k=﹣3<0,
∴W随m的增大而减小,
∴当m=50时,W最少=2090万元,即第三种方案费用最少
(3)解:在(2)的基础上有:W=(25+a)m+28×(80﹣m)=(a﹣3)m+2240
当a=3时,三种方案的费用一样,都是2240万元.
当a>3时,k=a﹣3>0,
∴W随m的增大而增大,
∴m的值越小时,费用W最小.
当0<a<3时,k=a﹣3<0,
∴W随m的增大而减小,
∴m的值越大时,W最小,费用最省
【解析】(1)设甲种套房每套提升费用为x万元,根据题意建立方程求出其解即可;(2)设甲种套房提升m套,那么乙种套房提升(80﹣m)套,根据条件建立不等式组求出其解就可以求出提升方案,再表示出总费用与m之间的函数关系式,根据一次函数的性质就可以求出结论;(3)根据(2)表示出W与m之间的关系式,由一次函数的性质分类讨论就可以得出结论.
【考点精析】本题主要考查了分式方程的应用和一元一次不等式组的应用的相关知识点,需要掌握列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位);1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圆锥纸帽的侧面展开图是一个圆心角为120°,弧长为6π(cm)的扇形纸片,则圆锥形纸帽的侧面积为( )
A.9π cm2
B.18π cm2
C.27π cm2
D.36π cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y= ![]() x+b与双曲线y=
x+b与双曲线y= ![]() 的一个交点为(2,5),直线与y轴交于点A.
的一个交点为(2,5),直线与y轴交于点A. 
(1)求m的值及点A的坐标;
(2)若点P在双曲线y= ![]() 的图象上,且S△POA=10,求点P的坐标.
的图象上,且S△POA=10,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在黑板上出了一道解方程的题![]() ,小虎马上举手,要求到黑板上去做,他是这样做的:
,小虎马上举手,要求到黑板上去做,他是这样做的:
5(3x-1)=2(4x+2)-1①,
15x-5=8x+4-1②,
15x-8x=4-1+5③
7x④,
x=![]() ⑤
⑤
老师说:小虎解一元一次方程的一般步骤都知道,但没有掌握好,因此解题出现了错误,请指出他的错步及错误原因: ,方程的正确的解是x= .
然后,你自己细心的解下面的方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABGD中,AB=AD=6,梯形ABCD中,DE⊥DC交AB于E,DF平分∠EDC交BC于F,连结EF. 
(1)证明:EF=CF;
(2)当 ![]() 时,求EF的长.
时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课题小组为了解某品牌手机的销售情况,对某专卖店该品牌手机在今年1~4月的销售做了统计,并绘制成如图两幅统计图(如图). 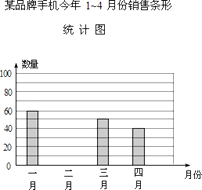

(1)该专卖店1~4月共销售这种品牌的手机台;
(2)请将条形统计图补充完整;
(3)在扇形统计图中,“二月”所在的扇形的圆心角的度数是;
(4)在今年1~4月份中,该专卖店售出该品牌手机的数量的中位数是台.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,路灯OP距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B处时,人影的长度( ) 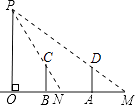
A.变长了1.5米
B.变短了2.5米
C.变长了3.5米
D.变短了3.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年2月18日韩国海军海警在朝鲜半岛东部海域实施联合演习,在返回济州岛军事基地途中,韩国海军UH﹣60直升机在距海平面垂直高度为300米的点C处测得济州一小岛的西端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了3500米,在点D测得这小岛的东端点B的俯角为45°,求这个济州小岛东西两端BA的距离(结果精确到1米,参考数据: ![]() ≈1.732,
≈1.732, ![]() ≈1.414)
≈1.414)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com