
【题目】如图,正方形ABGD中,AB=AD=6,梯形ABCD中,DE⊥DC交AB于E,DF平分∠EDC交BC于F,连结EF. 
(1)证明:EF=CF;
(2)当 ![]() 时,求EF的长.
时,求EF的长.
【答案】
(1)证明:∵正方形ABGD,
又∵DE⊥DC,
∴∠ADE+∠EDG=90°=∠GDC+∠EDG,
∴∠ADE=∠GDC.
又∵∠A=∠DGC,
且AD=GD,
在△ADE与△GDC中,
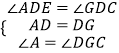 ,
,
∴△ADE≌△GDC(ASA).
∴DE=DC,且AE=GC.
在△EDF和△CDF中,
 ,
,
∴△EDF≌△CDF(SAS).
∴EF=CF
(2)解:∵ ![]() ,
,
∴AE=GC=2.
设EF=x,则BF=8﹣CF=8﹣x,BE=6﹣2=4.
由勾股定理,得x2=(8﹣x)2+42.
解之,得x=5,
即EF=5
【解析】(1)根据正方形的性质和全等三角形的判定和性质证明即可;(2)设EF=x,根据勾股定理解答即可.
【考点精析】关于本题考查的正方形的性质,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】已知:如图,已知△ABC 中,其中 A(0,﹣2),B(2,﹣4),C(4,﹣1).
(1)画出与△ABC 关于 y 轴对称的图形△A1B1C1;
(2)写出△A1B1C1 各顶点坐标;
(3)求△ABC 的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB外的一点,点Q是点P关于OA的对称点,点R是点P关于OB的对称点,直线QR分别交∠AOB两边OA,OB于点M,N,连结PM,PN,如果∠PMO=33°,∠PNO=70°,求∠QPN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级(1)班的宣传委员在办黑板报时,采用了下面的图案作为边框,其中每个黑色六边形与6个白色六边形相邻.若一段边框上有45个黑色六边形,则这段边框共有白色六边形( )

A. 182个 B. 180个 C. 272个 D. 270个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
(3)在(2)的条件下,根据市场调查,每套乙种套房的提升费用不会改变,每套甲种套房提升费用将会提高a万元(a>0),市政府如何确定方案才能使费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D. 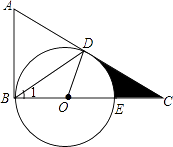
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数 ![]() 的图象上.若点A的坐标为(﹣2,﹣2),则k的值为 .
的图象上.若点A的坐标为(﹣2,﹣2),则k的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中AB=3,BC=4,∠B=90°,点B、C在两坐标轴上滑动.当边AC⊥x轴时,点A刚好在双曲线 ![]() 上,此时下列结论不正确的是( )
上,此时下列结论不正确的是( )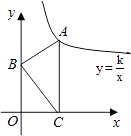
A.点B为(0, ![]() )
)
B.AC边的高为 ![]()
C.双曲线为 ![]()
D.此时点A与点O距离最大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com