
【题目】如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D. 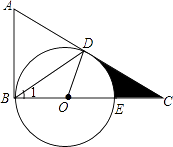
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
【答案】
(1)证明:连接OD,
∵OD=OB,
∴∠1=∠ODB,
∴∠DOC=∠1+∠ODB=2∠1,
而∠A=2∠1,
∴∠DOC=∠A,
∵∠A+∠C=90°,
∴∠DOC+∠C=90°,
∴OD⊥DC,
∴AC是⊙O的切线
(2)解:∵∠A=60°,
∴∠C=30°,∠DOC=60°,
在Rt△DOC中,OD=2,
∴CD= ![]() OD=2
OD=2 ![]() ,
,
∴阴影部分的面积=S△COD﹣S扇形DOE
= ![]() ×2×2
×2×2 ![]() ﹣
﹣ ![]()
=2 ![]() ﹣
﹣ ![]()
【解析】(1)由OD=OB得∠1=∠ODB,则根据三角形外角性质得∠DOC=∠1+∠ODB=2∠1,而∠A=2∠1,所以∠DOC=∠A,由于∠A+∠C=90°,所以∠DOC+∠C=90°,则可根据切线的判定定理得到AC是⊙O的切线;(2)由∠A=60°得到∠C=30°,∠DOC=60°,根据含30度的直角三角形三边的关系得CD= ![]() OD=2
OD=2 ![]() ,然后利用阴影部分的面积=S△COD﹣S扇形DOE和扇形的面积公式求解.
,然后利用阴影部分的面积=S△COD﹣S扇形DOE和扇形的面积公式求解.
【考点精析】根据题目的已知条件,利用切线的判定定理和扇形面积计算公式的相关知识可以得到问题的答案,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)5m-7n-8p+5n-9m-p;
(2)x4x5(-x)7+5(x4)4-(x7)3÷x5.
【答案】(1)-4m-2n-9p;(2)3x16
【解析】
(1)先移项,再合并同类项;
(2)原式利用幂的乘方、同底数幂的乘法和除法法则计算,再合并即可得到结果.
(1)5m-7n-8p+5n-9m-p=5m-9m-7n+5n-8p-p=-4m-2n-9p;
(2)x4x5(-x)7+5(x4)4-(x7)3÷x5=- x4x5x7+5x16-x21÷x5=- x16 +5x16-x16=3x16
【点睛】
此题考查了幂的乘方、同底数幂的乘法、除法法则计算以及合并同类项,熟练掌握整式运算的有关法则是解答此题的关键.
【题型】解答题
【结束】
21
【题目】解方程:![]() (x-2)-
(x-2)-![]() (4x-1)=4.
(4x-1)=4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y= ![]() x+b与双曲线y=
x+b与双曲线y= ![]() 的一个交点为(2,5),直线与y轴交于点A.
的一个交点为(2,5),直线与y轴交于点A. 
(1)求m的值及点A的坐标;
(2)若点P在双曲线y= ![]() 的图象上,且S△POA=10,求点P的坐标.
的图象上,且S△POA=10,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABGD中,AB=AD=6,梯形ABCD中,DE⊥DC交AB于E,DF平分∠EDC交BC于F,连结EF. 
(1)证明:EF=CF;
(2)当 ![]() 时,求EF的长.
时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课题小组为了解某品牌手机的销售情况,对某专卖店该品牌手机在今年1~4月的销售做了统计,并绘制成如图两幅统计图(如图). 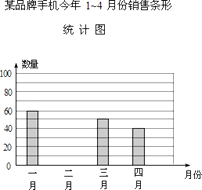

(1)该专卖店1~4月共销售这种品牌的手机台;
(2)请将条形统计图补充完整;
(3)在扇形统计图中,“二月”所在的扇形的圆心角的度数是;
(4)在今年1~4月份中,该专卖店售出该品牌手机的数量的中位数是台.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场打折前,买1件A商品和1件B商品用了20元,买30件A商品和40件B商品用了680元.打折后,买100件A商品100件B商品用了1800元.请根据上述信息解决下列问题:
(1)打折前A、B两种商品的单价分别是多少?
(2)请在(1)的基础上提出一个能使题目剩余条件解决的问题,并加以解决.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,路灯OP距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B处时,人影的长度( ) 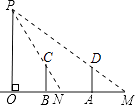
A.变长了1.5米
B.变短了2.5米
C.变长了3.5米
D.变短了3.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万安县开发区某电子电路板厂到井冈山大学从应届毕业生中招聘公司职员,对应聘者的专业知识、英语水平、参加社会实践与社团活动等三项进行测试或成果认定,三项的得分满分都为100分,三项的分数分别按5∶3∶2的比例记入每人的最后总分,有4位应聘者的得分如下表所示.
| 专业知识 | 英语水平 | 参加社会实践与 社团活动等 |
甲 | 85 | 85 | 90 |
乙 | 85 | 85 | 70 |
丙 | 80 | 90 | 70 |
丁 | 90 | 90 | 50 |
(1)分别算出4位应聘者的总分;
(2)表中四人“专业知识”的平均分为85分,方差为12.5,四人“英语水平”的平均分为87.5分,方差为6.25,请你求出四人“参加社会实践与社团活动等”的平均分及方差;
(3)分析(1)和(2)中的有关数据,你对大学生应聘者有何建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10,BC=12,点D在边BC上,且BD=4,以点D为顶点作∠EDF=∠B,分别交边AB于点E,交AC或延长线于点F. 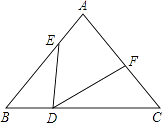
(1)当AE=4时,求AF的长;
(2)当以边AC为直径的⊙O与线段DE相切时,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com