
【题目】为加强防汛工作,某市对一拦水坝进行加固,如图,加固前拦水坝的横断面是梯形ABCD.已知迎水坡面AB=12米,背水坡面CD=12 ![]() 米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tanE=
米,∠B=60°,加固后拦水坝的横断面为梯形ABED,tanE= ![]() ,则CE的长为米.
,则CE的长为米.
【答案】8
【解析】解:分别过A、D作AF⊥BC,DG⊥BC,垂点分别为F、G,如图所示.
∵在Rt△ABF中,AB=12米,∠B=60°,
∴sin∠B= ![]() ,
,
∴AF=12× ![]() =6
=6 ![]() ,
,
∴DG=6 ![]() .
.
∵在Rt△DGC中,CD=12 ![]() ,DG=6
,DG=6 ![]() 米,
米,
∴GC= ![]() =18.
=18.
∵在Rt△DEG中,tanE= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴GE=26,
∴CE=GE﹣CG=26﹣18=8.
即CE的长为8米.
所以答案是8.
【考点精析】掌握关于坡度坡角问题是解答本题的根本,需要知道坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连接EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连接CG. 
(1)试说明四边形EFCG是矩形;
(2)当圆O与射线BD相切时,点E停止移动,在点E移动的过程中, ①矩形EFCG的面积是否存在最大值或最小值?若存在,求出这个最大值或最小值;若不存在,说明理由;
②求点G移动路线的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )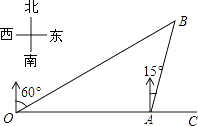
A.4km
B.2 ![]() km
km
C.2 ![]() km
km
D.( ![]() +1)km
+1)km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,自来水厂A和村庄B在小河l的两侧,现要在A,B间铺设一条输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏西49°方向,B位于南偏西41°方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A,B间的距离.(参考数据cos41°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江汉平原享有“中国小龙虾之乡”的美称,甲、乙两家农贸商店,平时以同样的价格出售品质相同的小龙虾,“龙虾节”期间,甲、乙两家商店都让利酬宾,付款金额y甲、y乙(单位:元)与原价x(单位:元)之间的函数关系如图所示: 
(1)直接写出y甲 , y乙关于x的函数关系式;
(2)“龙虾节”期间,如何选择甲、乙两家商店购买小龙虾更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣3,4),B(﹣5,2),C(﹣2,1).
(1)画出△ABC关于y轴对称图形△A1B1C1;
(2)画出将△ABC绕原点O逆时针方向旋转90°得到的△A2B2C2;
(3)求(2)中线段OA扫过的图形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】贵州省是我国首个大数据综合试验区,大数据在推动经济发展、改善公共服务等方面日益显示出巨大的价值,为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是部分四类生活信息关注度统计图表,请根据图中提供的信息解答下列问题: 
(1)本次参与调查的人数有人;
(2)关注城市医疗信息的有人,并补全条形统计图;
(3)扇形统计图中,D部分的圆心角是度;
(4)说一条你从统计图中获取的信息.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com