
【题目】如图,在平行四边形ABCD中,AC=CD.点E、F分别为边BC、CD上的两点,且∠EAF=∠CAD
(1)求证:∠D=∠ACB:
(2)求证:△ADF∽△ACE:
(3)求证:AE=EF.
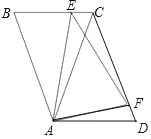
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)根据平行四边形性质得出∠ACB=∠CAD,再利用等边对等角可以得到∠D=∠CAD,进一步得出证明;
(2)根据两组角对应相等的两个三角形相等证明相似即可;
(3)根据△ADF∽△ACE得出对应边成比例,然后进一步证明△EAF∽△CAD,所以∠EFA=∠D,最后进一步证明即可.
证明:(1)∵AC=CD,
∴∠D=∠CAD,
∵四边形ABCD为平行四边形,
∴BC∥AD,
∴∠ACB=∠CAD,
∴∠D=∠ACB;
(2)∵∠EAF=∠CAD,
∴∠EAC=∠DAF,
又∵∠D=∠ACB,
∴△ADF∽△ACE:
(3)∵△ADF∽△ACE,
∴AD:AC=AF:AE,
∴AD:AF=AC:AE,
∵∠EAF=∠CAD,
∴△EAF∽△CAD,
∴∠EFA=∠D,
∴∠EAF=∠EFA,
∴EA=EF.


科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象相交于点A(1,4)和B(﹣2,n).
的图象与一次函数y2=ax+b的图象相交于点A(1,4)和B(﹣2,n).
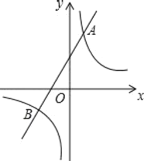
(1)求反比例函数与一次函数的解析式;
(2)请根据图象直接写出y1<y2时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为6,点
的边长为6,点![]() 是
是![]() 边的中点,连接
边的中点,连接![]() 与对角线
与对角线![]() 交于点
交于点![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 。以下结论:①
。以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 。其中正确的结论是( )
。其中正确的结论是( )
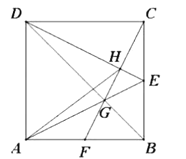
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某一个函数给出如下定义:若存在实数![]() ,对于任意的函数值
,对于任意的函数值![]() ,都满足
,都满足![]() ,则称这个函数是有界函数,在所有满足条件的
,则称这个函数是有界函数,在所有满足条件的![]() 中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.
中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.

(1)分别判断函数![]()
![]() 和
和![]() 是不是有界函数?若是有界函数,求其边界值;
是不是有界函数?若是有界函数,求其边界值;
(2)若函数![]()
![]() 的边界值是2,且这个函数的最大值也是2,求
的边界值是2,且这个函数的最大值也是2,求![]() 的取值范围;
的取值范围;
(3)将函数![]() 的图象向下平移
的图象向下平移![]() 个单位,得到的函数的边界值是
个单位,得到的函数的边界值是![]() ,当
,当![]() 在什么范围时,满足
在什么范围时,满足![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
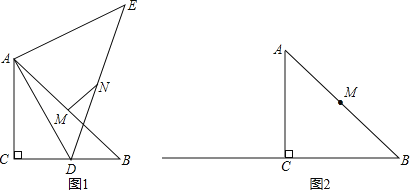
【题目】如图,等腰直角三角形ABC中,∠ACB=90°.D为射线BC上一动点.连接AD,将线段AD绕点A逆时针旋转90°至点E,连接AE、DE.点M、N分别是AB、DE的中点,连接MN.
(1)如图1,点D在线段BC上.
①猜想MN与AB的位置关系,并证明你的猜想;
②连接EB,猜想BE与BC的位置关系;
(2)在图2中,若点D在线段BC的延长线上,BE与BC的位置关系是否改变?请你补全图形后,证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且-2≤x≤1时,y的最大值为9,则a的值为![]()
![]()
A. 1或![]() B. -
B. -![]() 或
或![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年9月,我国中小学生迎来了新版“教育部统编义务教育语文教科书”,本次“统编本”教材最引人关注的变化之一是强调对传统文化经典著作的阅读,某校对A《三国演义》、B《红楼梦》、C《西游记》、D《水浒》四大名著开展“最受欢迎的传统文化经典著作”调查,随机调查了若干名学生(每名学生必选且只能选这四大名著中的一部)并将得到的信息绘制了下面两幅不完整的统计图:

(1)本次一共调查了 名学生;
(2)请将条形统计图补充完整;
(3)某班语文老师想从这四大名著中随机选取两部作为学生暑期必读书籍,请用树状图或列表的方法求恰好选中《三国演义》和《红楼梦》的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD(四边相等、四内角相等)中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=4,BE=DF=3,则EF的平方为( )

A.2B.![]() C.3D.4
C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com