
【题目】如图,正方形![]() 的边长为6,点
的边长为6,点![]() 是
是![]() 边的中点,连接
边的中点,连接![]() 与对角线
与对角线![]() 交于点
交于点![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 。以下结论:①
。以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 。其中正确的结论是( )
。其中正确的结论是( )
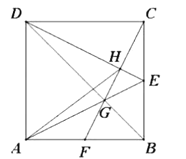
A.1B.2C.3D.4
【答案】D
【解析】
根据正方形对角线的性质及全等三角形的性质求证![]() ,从而判断①;延长DE,AB相交于点M,根据条件证出△DCH∽△MFH,从而判断②;根据勾股定理及三角形面积公式求得
,从而判断①;延长DE,AB相交于点M,根据条件证出△DCH∽△MFH,从而判断②;根据勾股定理及三角形面积公式求得![]() ,然后根据△DCG∽△BFG求得
,然后根据△DCG∽△BFG求得![]() ,从而判断④,过点H作HK⊥AB,利用勾股定理和相似三角形的性质求得
,从而判断④,过点H作HK⊥AB,利用勾股定理和相似三角形的性质求得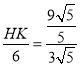 ,
,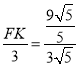 ,求得
,求得![]() ,从而判断③.
,从而判断③.
解:由题意可知:![]()
又∵正方形ABCD中,AB=CB,BG=BG
∴△ABG≌△CBG
∴![]()
又∵点E是BC的中点,
∴CE=BE
又∵正方形ABCD中,AB=CD,![]()
∴△DCE≌△ABE
∴![]()
∵![]()
∴![]() ,即①
,即①![]() 正确;
正确;
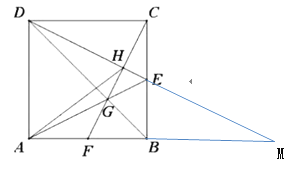
如图:延长DE,AB相交于点M
∵在正方形ABCD中,点E是BC的中点,
∴易证△DCE≌△MBE
∴DC=BM=6
又由①![]() 正确
正确
可得![]()
又∵![]()
∴△DCE≌△CBF
∴BF=CE=3
∵DC∥AB
∴△DCH∽△MFH
∴![]()
∴②![]() 正确;
正确;
由题意可知CE=3,DC=6,∠DCE=90°
∴![]()
又根据三角形面积公式可得:![]()
∴![]()
由△DCE≌△CBF
∴CF=DE
∵DC∥AB
∴△DCG∽△BFG
∴![]() ,即
,即![]()
∴![]()
∴![]() ,④正确.
,④正确.
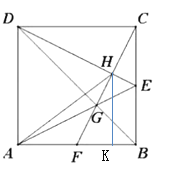
过点H作HK⊥AB
由易证可知![]()
∴![]() ,即
,即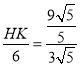
∴![]()
同理:![]() ,即
,即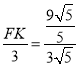
∴![]()
∴![]()
∴在Rt△AHK中,![]()
∴③![]() 正确;正确的共4个,
正确;正确的共4个,
故选:D.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=-![]() x2+
x2+![]() x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C:连接BC,点P为线段BC上方抛物线上的一动点,连接OP交BC于点Q.
x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C:连接BC,点P为线段BC上方抛物线上的一动点,连接OP交BC于点Q.
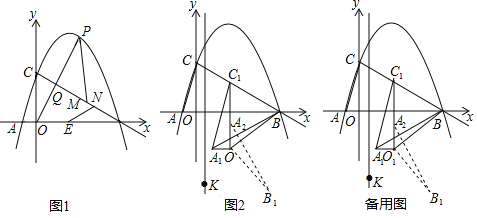
(1)如图1,当![]() 值最大时,点E为线段AB上一点,在线段BC上有两动点M,N(M在N上方),且MN=1,求PM+MN+NE-
值最大时,点E为线段AB上一点,在线段BC上有两动点M,N(M在N上方),且MN=1,求PM+MN+NE-![]() BE的最小值;
BE的最小值;
(2)如图2,连接AC,将△AOC沿射线CB方向平移,点A,C,O平移后的对应点分别记作A1,C1,O1,当C1B=O1B时,连接A1B、O1B,将△A1O1B绕点O1沿顺时针方向旋转90°后得△A2O1B1在直线x=![]() 上是否存在点K,使得△A2B1K为等腰三角形?若存在,直接写出点K的坐标;不存在,请说明理由.
上是否存在点K,使得△A2B1K为等腰三角形?若存在,直接写出点K的坐标;不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(﹣3,0),C(1,0),BC=![]() AC.
AC.
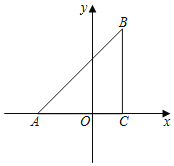
(1)在x轴上找一点D,连接DB,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;
(2)在(1)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m,使得△APQ与△ADB相似?如存在,请求出m的值;如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,垂足为E,如果AB=5,AE=4,BC=8,有下列结论:
①DE=4![]() ;
;
②S△AED=![]() S四边形ABCD;
S四边形ABCD;
③DE平分∠ADC;
④∠AED=∠ADC.
其中正确结论的序号是_____(把所有正确结论的序号都填在横线上)

查看答案和解析>>
科目:初中数学 来源: 题型:
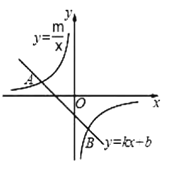
【题目】如图,已知![]() 是一次函数
是一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的两个交点。
的图象的两个交点。
(1)求此反比例函数和一次函数的解析式;
(2)连接![]() ,求
,求![]() 的面积;
的面积;
(3)根据图象直接写出使不等式![]() 成立的
成立的![]() 的取值范围______________________。
的取值范围______________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
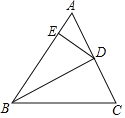
【题目】如图,在△ABC中,点BD⊥AC于点D,DE⊥AB于点E,BD2=BCBE.
(1)求证:△BCD∽△BDE;
(2)如果BC=10,AD=6,求AE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
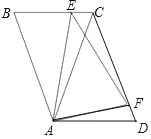
【题目】如图,在平行四边形ABCD中,AC=CD.点E、F分别为边BC、CD上的两点,且∠EAF=∠CAD
(1)求证:∠D=∠ACB:
(2)求证:△ADF∽△ACE:
(3)求证:AE=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
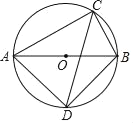
【题目】如图,△ABC内接于⊙O,AB是⊙O直径,∠ACB的平分线交⊙O于D,若AC=m,BC=n,则CD的长为_____(用含m、n的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com