
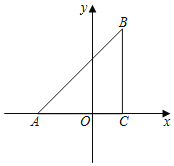
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�У���ABC��ֱ�������Σ���ACB��90������A��C������ֱ�ΪA����3��0����C��1��0����BC��![]() AC��
AC��
��1����x������һ��D������DB��ʹ����ADB����ABC���ƣ�������ȫ�ȣ��������D�����ꣻ
��2���ڣ�1���������£���P��Q�ֱ���AB��AD�ϵĶ��㣬����PQ����AP��DQ��m�����Ƿ����������m��ʹ����APQ����ADB���ƣ�����ڣ������m��ֵ���粻���ڣ���˵�����ɣ�
���𰸡���1����![]() ��0������2�����ڣ���m��
��0������2�����ڣ���m��![]() ��
��![]() ʱ����APQ����ADB���ƣ����ɼ�����
ʱ����APQ����ADB���ƣ����ɼ�����
��������
��1����ͼ1������B��BD��AB����x���ڵ�D����֤��ABC�ס�ADB���ɵ���ABC����ADB����֤��ABC�ס�BDC���ɵ�![]() ������CD�ij����������D���ꣻ
������CD�ij����������D���ꣻ
��2��������������ۣ������������ε����ʿ���⣮
��1����ͼ1������B��BD��AB����x���ڵ�D��
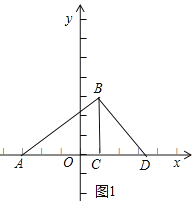
�ߡ�A����A����ACB����ABD��90����
���ABC�ס�ADB��
���ABC����ADB���ҡ�ACB����BCD��90����
���ABC�ס�BDC��
��![]()
��A����3��0����C��1��0����
��AC��4��
��BC��![]() AC��
AC��
��BC��3��
��AB��![]() ��
��![]() ��5��
��5��
��![]() ��
��
��![]() ��
��
��CD��![]() ��
��
��AD��AC+CD��4+![]() ��
��![]() ��
��
��OD��AD��AO��![]() ��
��
���D����������![]() ��0����
��0����
��2����ͼ2������APC����ABD��90��ʱ��
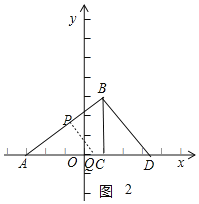
�ߡ�APC����ABD��90������BAD����PAQ��
���APQ�ס�ABD��
��![]() ��
��
��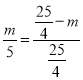
��m��![]() ��
��
��ͼ3������AQP����ABD��90��ʱ��
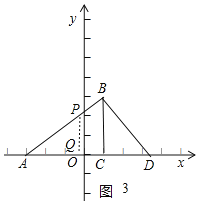
�ߡ�AQP����ABD��90������PAQ����BAD��
���APQ�ס�ADB��
��![]() ��
��
��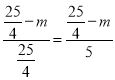
��m��![]() ��
��
������������m��![]() ��
��![]() ʱ����APQ����ADB���ƣ�
ʱ����APQ����ADB���ƣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�λ����Ϊ1�������������У�һ��Բ����������Ľ���A��B��C��
(1)��������²�����
���Ե�OΪԭ�㡢��ֱ��ˮƽ����Ϊ�ᡢ����߳�Ϊ��λ��������ƽ��ֱ������ϵ��
�ڸ���ͼ���ṩ����Ϣ�������Բ������Բ��Բ��D��������AD��CD
(2)����(1)�Ļ����ϣ����������գ�
��д��������꣺C______��D______��
�ڡ�D�İ뾶=______(�����������)
�������AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��˳�����ӶԽ�����ȵ��ı��θ����е㣬�����ı�����( )
A. ���� B. ƽ���ı��� C. ���� D. �����ı���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������y1��![]() ��ͼ����һ�κ���y2��ax+b��ͼ���ཻ�ڵ�A��1��4����B����2��n����
��ͼ����һ�κ���y2��ax+b��ͼ���ཻ�ڵ�A��1��4����B����2��n����
��1������������һ�κ����Ľ���ʽ��
��2�������ͼ��ֱ��д��y1��y2ʱ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺���һ������ƽ������![]() ����Ϊ
����Ϊ![]() ,�����
,�����![]() ����������λ����ô��������ѧ��ʵ����Ӧ�����ͽ�����������ʾΪ
����������λ����ô��������ѧ��ʵ����Ӧ�����ͽ�����������ʾΪ![]() ��
��![]() Ϊʵ������
Ϊʵ������![]() �����������ʵ����
�����������ʵ���� ![]() ��������������鲿�����ļӣ������˷���������ʽ�ļӣ������˷��������ơ�
��������������鲿�����ļӣ������˷���������ʽ�ļӣ������˷��������ơ�
������㣺 ![]()
��1����գ� ![]() =_________,
=_________, ![]() =____________.
=____________.
��2����գ���![]() _________�� ��
_________�� ��![]() _________ ��
_________ ��
��3��������������ȣ������ǵ�ʵ�����鲿����ֱ���ȣ�����������⣺��֪�� ![]() ����
���� ![]() Ϊʵ��������
Ϊʵ��������![]() ��ֵ��
��ֵ��
��4����һ�ԣ���������ǰѧϰ���й�֪ʶ��![]() �����
�����![]() ����ʽ��
����ʽ��
��5���ⷽ�̣�x2 - 2x +4 = 0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������ABCD�ĶԽ����ཻ��O.��M,N�ֱ��DZ�BC,CD�ϵĶ���(�����B,C,D�غ�),AM,AN�ֱ�BD��E,F����,�ҡ�MAN=45��,�����н���:��MN=BM+DN;�ڡ�AEF�ס�BEM;��![]() ;�ܡ�FMC�ǵ���������.������ȷ���У�������
;�ܡ�FMC�ǵ���������.������ȷ���У�������
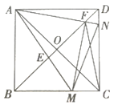
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A������Ϊ(0��4)����B������Ϊ(4��4)����C������Ϊ(4��0)����D��x����(�ڵ�O�Ҳ�)����һ�㣬��ADΪ�����Ҳ���������ADEF������BF�����D������Ϊ(t��0)��.
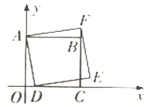
(1)��֤����AOD�ա�ABF��
(2)���E������(�ú���t�Ĵ���ʽ����ʾ)��
(3)����DBE�ǵ���������ʱ����ֱ��д��t��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �ı߳�Ϊ6����
�ı߳�Ϊ6����![]() ��
��![]() �ߵ��е㣬����
�ߵ��е㣬����![]() ��Խ���
��Խ���![]() ���ڵ�
���ڵ�![]() ������
������![]() ���ӳ�����
���ӳ�����![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() �����½��ۣ���
�����½��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ��������ȷ�Ľ����ǣ� ��
��������ȷ�Ľ����ǣ� ��
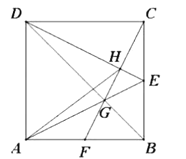
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() Ϊ
Ϊ![]() ��ֱ����
��ֱ����![]() Ϊ
Ϊ![]() ��һ�㣬
��һ�㣬![]() ����
����![]() �������ഹֱ������Ϊ
�������ഹֱ������Ϊ![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
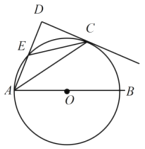
��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2������![]() ����
����![]() ��
��![]() �����
�����![]() ��ֱ���ij���
��ֱ���ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com