
【题目】如图,在平面直角坐标系中,点A的坐标为(0,4),点B的坐标为(4,4),点C的坐标为(4,0),点D是x轴上(在点O右侧)任意一点,以AD为边向右侧作正方形ADEF,连接BF,设点D的坐标为(t,0)处.
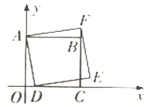
(1)求证:△AOD≌△ABF;
(2)求点E的坐标(用含有t的代数式来表示);
(3)当△DBE是等腰三角形时,请直接写出t的值.
【答案】(1) 见解析;(2) E(4+t,t) (3) 2,4,8.
【解析】
(1)由四边形ABCO和ADFE是正方形,得∠AOD=∠ABF=90°,AO=AB=4,AD=AF,即可利用HL证明△AOD≌△ABF;
(2)过点E作EH⊥x轴于点H,然后证明△AOD≌△DHE,得到DH=OA=4,OD=EH=t,即可得到点E的坐标;
(3)由(2)知点D为(t,0),点B为(4,4),点E为(4+t,t),利用勾股定理求出BD、BE、DE的长度,由△DBE是等腰三角形时,可分为三种情况进行讨论,即当BD=DE,BD=BE,DE=BE时,求出t的值即可.
(1)证明:根据题意,OA=OC=AB=BC=4,∠AOC=90°,
∴四边形ABCO是正方形,
∴∠AOC=∠ABF=90°,
∵四边形ADEF是正方形,
∴AD=AF,
∴△AOD≌△ABF(HL);
(2)解:如图:过点E作EH⊥x轴于点H,

∵∠AOD=∠ADE=90°,
∴∠OAD+∠ADO=∠EDH+∠ADO=90°,
∴∠OAD=∠EDH,
∵AD=DE,∠AOD=∠DHE=90°,
∴△AOD≌△DHE(AAS),
∴AO=DH=4,OD=EH=t,
∴OH=4+t,
∴点E的坐标为:(4+t,t);
(3)由(2)可知,点D为(t,0),点B为(4,4),点E为(4+t,t),
∴![]() ,
,![]() ,
,![]() ,
,
∵△DBE是等腰三角形,
当BD=DE时,有
![]() ,
,
解得:![]() ;
;
当BD=BE时,有
![]() ,
,
解得:![]() 或
或![]() (舍去);
(舍去);
当DE=BE时,有
![]() ,
,
解得:![]() 或
或![]() (舍去);
(舍去);
∴当![]() ,4或8时,△DBE是等腰三角形.
,4或8时,△DBE是等腰三角形.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
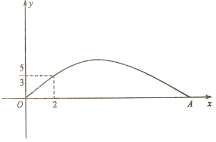
【题目】在某场足球比赛中,球员甲在球门正前方点O处起脚射门,在不受阻挡的情况下,足球沿如图所示的抛物线飞向球门中心线,当足球飞行的水平距离为2 m时,高度为![]() ,落地点A距O点12 m.已知点O距球门9 m,球门的横梁高为2.44 m.
,落地点A距O点12 m.已知点O距球门9 m,球门的横梁高为2.44 m.
(1)飞行的足球能否射入球门?通过计算说明理由;
(2)若守门员乙站在球门正前方2 m处,他跳起时能摸到的最大高度为2.52 m,他能阻止此次射门吗?并写明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成相应的任务:
我们知道,利用尺规作已知线段的垂直平分线可以得到该线段的中点、四等分点、……怎样得到线段的三等分点呢?如图,已知线段MN,用尺规在MN上求作点P,使![]() .
.
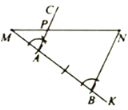
小颖的作法是:
①作射线MK(点K不在直线MN上);
②在射线MK上依次截取线段MA,AB,使![]() ,连接BN;
,连接BN;
③作射线![]() ,交MN于点P点P即为所求作的点.
,交MN于点P点P即为所求作的点.
小颖作法的理由如下:
∵![]() (作法),∴
(作法),∴![]()
∵![]() (已知),
(已知),![]() (等量代换)
(等量代换)
∵![]() (线段和差定义),∴
(线段和差定义),∴![]() (等量代换,等式性质)
(等量代换,等式性质)
数学思考:(1)小颖作法理由中所缺的依据是:________________________________.
拓展应用:(2)如图,已知线段a,b,c,求作线段d,使![]()
a. ![]() b.
b. ![]() c.
c. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(﹣3,0),C(1,0),BC=![]() AC.
AC.
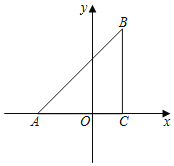
(1)在x轴上找一点D,连接DB,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;
(2)在(1)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m,使得△APQ与△ADB相似?如存在,请求出m的值;如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后D的对应点D2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,垂足为E,如果AB=5,AE=4,BC=8,有下列结论:
①DE=4![]() ;
;
②S△AED=![]() S四边形ABCD;
S四边形ABCD;
③DE平分∠ADC;
④∠AED=∠ADC.
其中正确结论的序号是_____(把所有正确结论的序号都填在横线上)

查看答案和解析>>
科目:初中数学 来源: 题型:
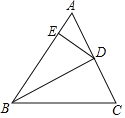
【题目】如图,在△ABC中,点BD⊥AC于点D,DE⊥AB于点E,BD2=BCBE.
(1)求证:△BCD∽△BDE;
(2)如果BC=10,AD=6,求AE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P的坐标为(![]() ,
,![]() ),点Q的坐标为(
),点Q的坐标为(![]() ,
,![]() ),且
),且![]() ,
,![]() ,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.下图为点P,Q 的“相关矩形”的示意图.
,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”.下图为点P,Q 的“相关矩形”的示意图.
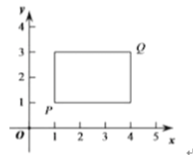
(1)已知点A的坐标为(1,0).
①若点B的坐标为(3,1)求点A,B的“相关矩形”的面积;
②点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(2)⊙O的半径为![]() ,点M的坐标为(m,3).若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
,点M的坐标为(m,3).若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com