
【题目】如图,正方形ABCD的对角线相交于O.点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于E,F两点,且∠MAN=45°,则下列结论:①MN=BM+DN;②△AEF∽△BEM;③![]() ;④△FMC是等腰三角形.其中正确的有( )
;④△FMC是等腰三角形.其中正确的有( )
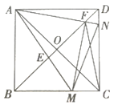
A.1个B.2个C.3个D.4个
【答案】D
【解析】
将△ABM绕点A逆时针旋转90°至△ADM′,根据正方形的性质和且∠MAN=45°可证明MN=BM+DN;根据三角形的内角和得到∠M′+∠AFD=180°,得到∠AFE=∠M′,推出∠AMB=∠AFE,于是得到△AEF∽△BEM,故②正确;根据相似三角形的判定定理得到△AEB∽△FEM,根据相似三角形的性质得到∠EMF=∠ABE=45°,推出△AFM是等腰直角三角形,于是得到![]() ;故③正确;根据全等三角形的性质得到AF=CF,等量代换得到△FMC是等腰三角形,故④正确.
;故③正确;根据全等三角形的性质得到AF=CF,等量代换得到△FMC是等腰三角形,故④正确.
解:将△ABM绕点A逆时针旋转90°至△ADM′,
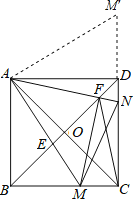
∵∠M′AN=∠DAN+∠MAB=45°,AM′=AM,BM=DM′,
∵∠M′AN=∠MAN=45°,AN=AN,
∴△AMN≌△AM′N′(SAS),
∴MN=NM′,
∴M′N=M′D+DN=BM+DN,
∴MN=BM+DN;故①正确;
∵∠FDM′=135°,∠M′AN=45°,
∴∠M′+∠AFD=180°,
∵∠AFE+∠AFD=180°,
∴∠AFE=∠M′,
∵∠AMB=∠M′,
∴∠AMB=∠AFE,
∵∠EAF=∠EBM=45°,
∴△AEF∽△BEM,故②正确;
∴![]() ,即
,即![]() ,
,
∵∠AEB=∠MEF,
∴△AEB∽△FEM,
∴∠EMF=∠ABE=45°,
∴△AFM是等腰直角三角形,
∴![]() ;故③正确;
;故③正确;
在△ADF与△CDF中,
 ,
,
∴△ADF≌△CDF(SAS),
∴AF=CF,
∵AF=MF,
∴FM=FC,
∴△FMC是等腰三角形,故④正确;
故选:D.


科目:初中数学 来源: 题型:
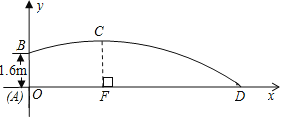
【题目】“阳光体育活动”促进了学校体育活动的开展,小杰在一次铅球比赛中,铅球出手以后的轨迹是抛物线的一部分(如图所示),已知铅球出手时离地面1.6米,铅球离投掷点3米时达到最高点,在离投掷点8米处落地,
(1)请求出此轨迹所在抛物线的关系式.
(2)设抛物线与X轴另一个交点是E,点Q是对称轴上的一个动点,求当△EBQ的周长最短时点Q的坐标.
(3)在抛物线上是否存在点G使得S△DEG=19.5,若存在请求出点G的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形OABC的边OA、OC分别在x轴、y轴上,B点坐标是(8,4),将△AOC沿对角线AC翻折得△ADC,AD与BC相交于点E.
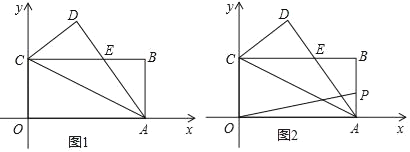
(1)求证:△CDE≌△ABE
(2)求E点坐标;
(3)如图2,动点P从点A出发,沿着折线A→B→C→O运动(到点O停止),是否存在点P,使得△POA的面积等于△ACE的面积,若存在,直接写出点P坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
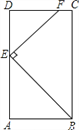
【题目】如图,在矩形ABCD中,AB=3,AD=6,点E在AD边上,且AE=4,EF⊥BE交CD于点F.
(1)求证:△ABE∽△DEF;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(﹣3,0),C(1,0),BC=![]() AC.
AC.
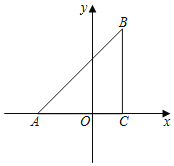
(1)在x轴上找一点D,连接DB,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;
(2)在(1)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m,使得△APQ与△ADB相似?如存在,请求出m的值;如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小涵和小西想要测量建筑物OP与广告牌AB的高度.首先,小涵站在D处看到广告牌AB的顶端A、建筑物OP的顶端O在一条直线上;然后,在阳光下,小西站在N处,此时他的影长为NE,同一时刻,测得建筑物OP的影长为PG,OP⊥PD,AB⊥PD,CD⊥PD,MN⊥PD.
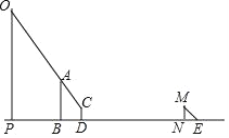
(1)请你画出表示建筑物OP在阳光下的影子PG;
(2)已知NE=1.92m,PG=24m,BD=3m,建筑物OP与广告牌AB之间的距离PB=8.1m,小涵的眼睛到地面的距离CD=1.5m,小西的身高MN=1.6m.
①求出建筑物OP的高度;
②求出广告牌AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
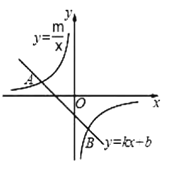
【题目】如图,已知![]() 是一次函数
是一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的两个交点。
的图象的两个交点。
(1)求此反比例函数和一次函数的解析式;
(2)连接![]() ,求
,求![]() 的面积;
的面积;
(3)根据图象直接写出使不等式![]() 成立的
成立的![]() 的取值范围______________________。
的取值范围______________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2),
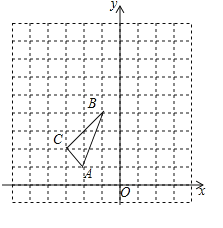
(1)画△ABC关于y轴对称的图形△A1B1C1;
(2)以O为位似中心,在第二象限内把△ABC扩大到原来的两倍,得则△A2B2C2,画出△A2B2C2;
(3)△ABC的面积为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com