
【题目】如图,小涵和小西想要测量建筑物OP与广告牌AB的高度.首先,小涵站在D处看到广告牌AB的顶端A、建筑物OP的顶端O在一条直线上;然后,在阳光下,小西站在N处,此时他的影长为NE,同一时刻,测得建筑物OP的影长为PG,OP⊥PD,AB⊥PD,CD⊥PD,MN⊥PD.
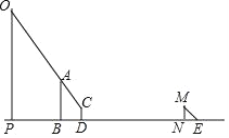
(1)请你画出表示建筑物OP在阳光下的影子PG;
(2)已知NE=1.92m,PG=24m,BD=3m,建筑物OP与广告牌AB之间的距离PB=8.1m,小涵的眼睛到地面的距离CD=1.5m,小西的身高MN=1.6m.
①求出建筑物OP的高度;
②求出广告牌AB的高度.
【答案】(1)如图所示,PG即为所求;见解析;(2)①建筑物OP的高度为20m;②广告牌AB的高度为6.5m.
【解析】
(1)过点O作ME的平行线,交PE于点G,即可得;
(2)①由△OGP∽△MEN知![]() ,即
,即![]() ,解之可得;
,解之可得;
②作CF⊥OP,交AB于点H,证△OFC∽△AHC得![]() ,即
,即![]() ,求得AH的长,继而可得答案.
,求得AH的长,继而可得答案.
(1)如图所示,PG即为所求;
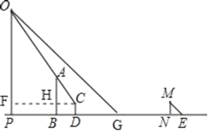
(2)①由题意知∠OPD=∠MNE,∠PGP=∠MEN,
∴△OGP∽△MEN,
∴![]() ,即
,即![]() ,
,
解得:OP=20m,
∴建筑物OP的高度为20m;
②过点C作CF⊥OP于点F,交AB于点H,

则∠OFC=∠AHC=90°,∠OCF=∠ACH,FH=PB=8.1m,HC=BD=PF=1.5m,OF=OP﹣PF=18.5m,
∴△OFC∽△AHC,
∴![]() ,即
,即![]() ,
,
∴AH=5m,AB=AH+BH=6.5m,
∴广告牌AB的高度为6.5m.


科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象记为
的图象记为![]() ,它与x轴交于点O,
,它与x轴交于点O,![]() ;将
;将![]() 绕点
绕点![]() 旋转
旋转![]() 得
得![]() ,交x轴于点
,交x轴于点![]() ;将
;将![]() 绕点
绕点![]() 旋转
旋转![]() 得
得![]() ,交x轴于点
,交x轴于点![]() ;……如此进行下去,得到一条“波浪线”.若
;……如此进行下去,得到一条“波浪线”.若![]() 在这条“波浪线”上,则
在这条“波浪线”上,则![]() ________.
________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方格图中的每个小方格都是边长为1小正方形,我们把小正方形的顶点称为格点,格点连线为边的四边形称为“格点四边形”,图1中的四边形ABCD就是一个格点四边形.
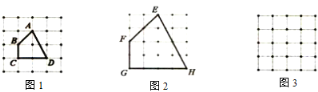
(1)小彬在图2的方格图中画了一个格点四边形EFGH.借助方格图回答:四边形ABCD与四边形EFGH相似吗?若相似,直接写出四边形ABCD与四边形EFGH的相似比;若不相似说明理由;
(2)请在图3的方格图中画一个格点四边形,使它与四边形ABCD相似,但与四边形ABCD、四边形EFGH都不全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
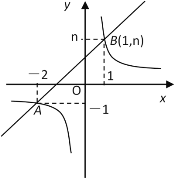
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A(-2,-1)、B(1,n)两点。
的图象交于A(-2,-1)、B(1,n)两点。
(1)利用图中条件求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于O.点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于E,F两点,且∠MAN=45°,则下列结论:①MN=BM+DN;②△AEF∽△BEM;③![]() ;④△FMC是等腰三角形.其中正确的有( )
;④△FMC是等腰三角形.其中正确的有( )
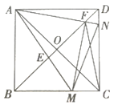
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交CD于点F,交AD的延长线于点E,若AB=4,BM=2,则△DEF的面积为( )
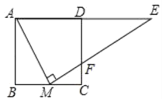
A.9B.8C.15D.14.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD的面积为10cm2,它的两条对角线交于点O1,以AB、AO1为邻边作平行四边形ABC1O1,平行四边形ABC1O1的对角线交于点O2;同样以AB、AO2为邻边作平行四边形ABC2O2,……依此类推,则平行四边形ABC5O5的面积为( )
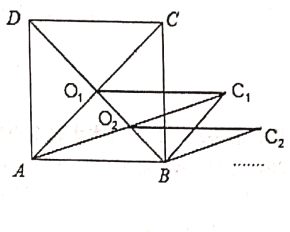
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E分别在边AB、AC上,DC与BE相交于点O,且DO=2,BO=DC=6,OE=3.
(1)求证:DE∥BC;
(2)如果四边形BCED的面积比△ADE的面积大12,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C为线段AB上一点,分别以AB、AC、CB为底作顶角为120°的等腰三角形,顶角顶点分别为D、E、F(点E、F在AB的同侧,点D在另一侧)
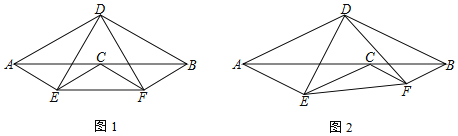
(1)如图1,若点C是AB的中点,则∠CED=______°;
(2)如图2.若点C不是AB的中点
①求证:△DEF为等边三角形;
②连接CD,若∠ADC=90°,AD=![]() ,请求出DE的长.
,请求出DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com