
【题目】如图,在△ABC中,点D,E分别在边AB、AC上,DC与BE相交于点O,且DO=2,BO=DC=6,OE=3.
(1)求证:DE∥BC;
(2)如果四边形BCED的面积比△ADE的面积大12,求△ABC的面积.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】如图4,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=2AD,F,E分别是AB,BC的中点,则下列结论不一定正确的是( )
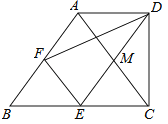
A.△ABC是等腰三角形B.四边形EFAM是菱形
C.![]() D.DE平分∠CDF
D.DE平分∠CDF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小涵和小西想要测量建筑物OP与广告牌AB的高度.首先,小涵站在D处看到广告牌AB的顶端A、建筑物OP的顶端O在一条直线上;然后,在阳光下,小西站在N处,此时他的影长为NE,同一时刻,测得建筑物OP的影长为PG,OP⊥PD,AB⊥PD,CD⊥PD,MN⊥PD.
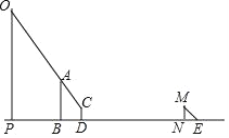
(1)请你画出表示建筑物OP在阳光下的影子PG;
(2)已知NE=1.92m,PG=24m,BD=3m,建筑物OP与广告牌AB之间的距离PB=8.1m,小涵的眼睛到地面的距离CD=1.5m,小西的身高MN=1.6m.
①求出建筑物OP的高度;
②求出广告牌AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个一次函数l1、l2的图象如图:

(1)分別求出l1、l2两条直线的函数关系式;
(2)求出两直线与y轴围成的△ABP的面积;
(3)观察图象:请直接写出当x满足什么条件时,l1的图象在l2的下方.
查看答案和解析>>
科目:初中数学 来源: 题型:
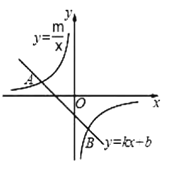
【题目】如图,已知![]() 是一次函数
是一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的两个交点。
的图象的两个交点。
(1)求此反比例函数和一次函数的解析式;
(2)连接![]() ,求
,求![]() 的面积;
的面积;
(3)根据图象直接写出使不等式![]() 成立的
成立的![]() 的取值范围______________________。
的取值范围______________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在Rt△ABC中,∠C=90°,AC=4,BC=3,O是AB上一点,且AO=2.
(1)求点O到直线AC的距离OH的长;
(2)若P是边AC上一个动点,作PQ⊥OP交线段BC于Q(不与B、C重合),设AP=x,CQ=y,试求y关于x的函数解析式,并写出定义域;
(3)在(2)的条件下,当AP为多少时能使△OPQ与△CPQ相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC顶点的坐标分别为A(1,-1),B(4,-1),C(3,-4).
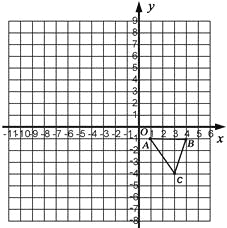
(1)将△ABC绕点A逆时针旋转90°后,得到△AB1C1.在所给的直角坐标系中画出旋转后的![]() ,并写出点
,并写出点![]() 的坐标:
的坐标:![]() ____________;
____________;
(2)以坐标原点O为位似中心,在第二象限内再画一个放大的![]() ,使得它与△ABC的位似比等于2:1 .
,使得它与△ABC的位似比等于2:1 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
(1)求∠DCE的度数;
(2)若AB=4,CD=3AD,求DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com