
【题目】如图4,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=2AD,F,E分别是AB,BC的中点,则下列结论不一定正确的是( )
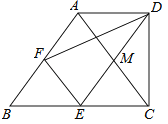
A.△ABC是等腰三角形B.四边形EFAM是菱形
C.![]() D.DE平分∠CDF
D.DE平分∠CDF
【答案】D
【解析】
试题连接AE,如图所示,

∵E为BC的中点,
∴BE=CE=![]() BC,又BC=2AD,
BC,又BC=2AD,
∴AD=BE=EC,又AD∥BC,
∴四边形ABED为平行四边形,四边形AECD为平行四边形,
又∵∠DCB=90°,
∴四边形AECD为矩形,
∴∠AEC=90°,即AE⊥BC,
∴AE垂直平分BC,
∴AB=AC,即△ABC为等腰三角形,
故选项A不合题意;
∵E为BC的中点,F为AB的中点,
∴EF为△ABC的中位线,
∴EF∥AC,EF=![]() AC,
AC,
又∵四边形ABED为平行四边形,
∴AF∥ME,
∴四边形AFEM为平行四边形,
又∵AF=![]() AB=
AB=![]() AC=EF,
AC=EF,
∴四边形AFEM为菱形,
故选项B不合题意;
过F作FN⊥BC于N点,可得FN∥AE,
又∵F为AB的中点,
∴N为BE的中点,
∴FN为△ABE的中位线,
∴FN=![]() AE,
AE,
又∵AE=DC,BE=AD,
∴S△BEF=![]() S△ACD,
S△ACD,
故选项C不合题意;
DE不一定平分∠CDF,
故选项D符合题意.
故选D.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】已知正方形![]() ,点
,点![]() 是其内部一点.
是其内部一点.

(1)如图1,点![]() 在边
在边![]() 的垂直平分线
的垂直平分线![]() 上,将
上,将![]() 绕点
绕点![]() 逆时针旋转,得到
逆时针旋转,得到![]() ,当点
,当点![]() 落在
落在![]() 上时,恰好点
上时,恰好点![]() 落在直线
落在直线![]() 上,求
上,求![]() 的度数;
的度数;
(2)如图2,点![]() 在对角线
在对角线![]() 上,连接
上,连接![]() ,若将线段
,若将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到线段
后得到线段![]() ,试问点
,试问点![]() 是否在直线
是否在直线![]() 上,请给出结论,并说明理由;
上,请给出结论,并说明理由;
(3)如图3,若![]() ,设
,设![]() ,
,![]() ,
,![]() ,请写出
,请写出![]() 、
、![]() 、
、![]() 这三条线段长之间满足的数量关系是____________.
这三条线段长之间满足的数量关系是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象记为
的图象记为![]() ,它与x轴交于点O,
,它与x轴交于点O,![]() ;将
;将![]() 绕点
绕点![]() 旋转
旋转![]() 得
得![]() ,交x轴于点
,交x轴于点![]() ;将
;将![]() 绕点
绕点![]() 旋转
旋转![]() 得
得![]() ,交x轴于点
,交x轴于点![]() ;……如此进行下去,得到一条“波浪线”.若
;……如此进行下去,得到一条“波浪线”.若![]() 在这条“波浪线”上,则
在这条“波浪线”上,则![]() ________.
________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个关于x的代数式A,若存在一个系数为正数关于x的单项式F,使![]() 的结果是所有系数均为整数的整式,则称单项式F为代数式A的“整系单项式”.例如:
的结果是所有系数均为整数的整式,则称单项式F为代数式A的“整系单项式”.例如:
当A=![]() ,F=2x3时,由于
,F=2x3时,由于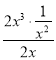 =1,故2x3是
=1,故2x3是![]() 的整系单项式;
的整系单项式;
当A=![]() ,F=6x5时,由于
,F=6x5时,由于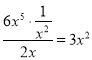 ,故6x5是
,故6x5是![]() 的整系单项式;
的整系单项式;
当A=3-![]() ,F=
,F=![]() 时,由于
时,由于 =2x-1,故
=2x-1,故![]() 是3-
是3-![]() 的整系单项式;
的整系单项式;
当A=3-![]() ,F=8x4时,由于
,F=8x4时,由于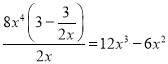 ,故8x4是3-
,故8x4是3-![]() 的整系单项式;
的整系单项式;
显然,当代数式A存在整系单项式F时,F有无数个,现把次数最低,系数最小的整系单项式F记为F(A).例如:![]() ,
,![]()
阅读以上材料并解决下列问题:
(1)判断:当A=![]() 时,F=2x3______A的整系单项式(填“是”或“不是”)
时,F=2x3______A的整系单项式(填“是”或“不是”)
(2)解方程: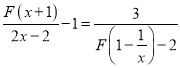
(3)已知a、b、c是△ABC的边长,其中a、b满足(a-5)2+![]() =0,且关于x的方程|
=0,且关于x的方程|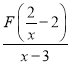 |=c有且只有3个不相等的实数根,求△ABC的周长.
|=c有且只有3个不相等的实数根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个小风筝与一个大风等形状完全相同,它们的形状如图所示,其中对角线AC⊥BD.已知它们的对应边之比为1:3,小风筝两条对角线的长分別为12cm和14cm.
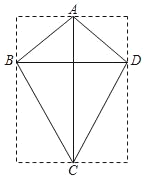
(1)小风筝的面积是多少?
(2)如果在大风筝内装设一个连接对角顶点的十字交叉形的支撑架,那么至少需用多长的材料?(不记损耗)
(3)大风筝要用彩色纸覆盖,而彩色纸是从一张刚好覆盖整个风筝的矩形彩色纸(如图中虚线所示)裁剪下来的,那么从四个角裁剪下来废弃不用的彩色纸的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方格图中的每个小方格都是边长为1小正方形,我们把小正方形的顶点称为格点,格点连线为边的四边形称为“格点四边形”,图1中的四边形ABCD就是一个格点四边形.
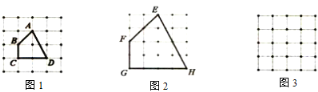
(1)小彬在图2的方格图中画了一个格点四边形EFGH.借助方格图回答:四边形ABCD与四边形EFGH相似吗?若相似,直接写出四边形ABCD与四边形EFGH的相似比;若不相似说明理由;
(2)请在图3的方格图中画一个格点四边形,使它与四边形ABCD相似,但与四边形ABCD、四边形EFGH都不全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
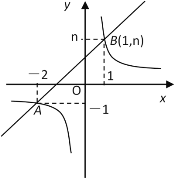
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A(-2,-1)、B(1,n)两点。
的图象交于A(-2,-1)、B(1,n)两点。
(1)利用图中条件求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E分别在边AB、AC上,DC与BE相交于点O,且DO=2,BO=DC=6,OE=3.
(1)求证:DE∥BC;
(2)如果四边形BCED的面积比△ADE的面积大12,求△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com