
【题目】如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
(1)求∠DCE的度数;
(2)若AB=4,CD=3AD,求DE的长.

【答案】解:(1)90°;(2)2![]()
【解析】
试题(1)首先由等腰直角三角形的性质求得∠BAD、∠BCD的度数,然后由旋转的性质可求得∠BCE的度数,故此可求得∠DCE的度数;
(2)由(1)可知△DCE是直角三角形,先由勾股定理求得AC的长,然后依据比例关系可得到CE和DC的长,最后依据勾股定理求解即可.
试题解析:(1)∵△ABCD为等腰直角三角形,
∴∠BAD=∠BCD=45°.
由旋转的性质可知∠BAD=∠BCE=45°.
∴∠DCE=∠BCE+∠BCA=45°+45°=90°.
(2)∵BA=BC,∠ABC=90°,
∴AC=![]() .
.
∵CD=3AD,
∴AD=![]() ,DC=3
,DC=3![]() .
.
由旋转的性质可知:AD=EC=![]() .
.
∴DE=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知点E,F分别是□ABCD的边BC,AD上的中点,且∠BAC=90°.
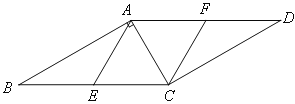
(1)求证:四边形AECF是菱形;
(2)若∠B=30°,BC=10,求菱形AECF面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:①二次函数y=ax2+bx+c的最小值为﹣4a;②若﹣1≤x2≤4,则0≤y2≤5a;③若y2>y1, 则x2>4;④一元二次方程cx2+bx+a=0的两个根为﹣1和![]() 其中正确结论的序号是( )
其中正确结论的序号是( )
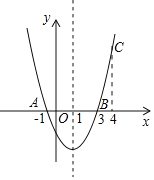
A.①④B.①②C.②③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种汽车刹车后行驶的距离s(单位:m)关于行驶的时间t(单位:s)的函数关系式为s=15t-at2,且t=1时,s=9.
(1)求s与t的函数关系式;
(2)该汽车刹车后到停下来前进了多远?
(3)该汽车刹车后前进6m时行驶了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】秋风送爽,学校组织同学们去颐和园秋游,昆明湖西堤六桥中的玉带桥最是令人喜爱,如图所示,玉带桥的桥拱是抛物线形水面宽度AB=10m,桥拱最高点C到水面的距离为6m.
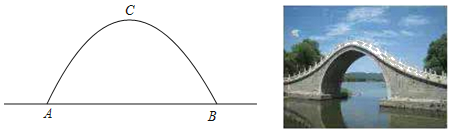
(1)建立适当的平面直角坐标系,求抛物线的表达式;
(2)现有一艘游船高度是4.5m,宽度是4m,为了保证安全,船顶距离桥拱顶部至少0.5m,通过计算说明这艘游船能否安全通过玉带桥.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过坐标原点O,与x轴交于另一点A,顶点为B.求:
经过坐标原点O,与x轴交于另一点A,顶点为B.求:
(1)抛物线的解析式;
(2)△AOB的面积;
(3)要使二次函数的图象过点(10,0),应把图象沿x轴向右平移 个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,CA=CB=6,∠ACB=120°,点D在线段AB上运动(不与A、B重合),将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,给出下列结论:
①CD=CP=CQ;②∠PCQ为定值;③△PCQ面积的最小值为![]() ;④当点D在AB的中点时,△PDQ是等边三角形,其中正确结论的个数为( )
;④当点D在AB的中点时,△PDQ是等边三角形,其中正确结论的个数为( )
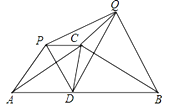
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com