
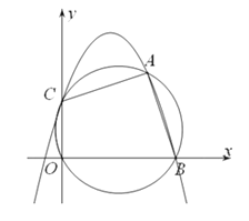
����Ŀ����ͼ�����κ���y=ax2+bx+c��ͼ����A����1��0������B��3��0������C��4��y1��������D��x2��y2����������������һ�㣬�����н��ۣ��ٶ��κ���y=ax2+bx+c����СֵΪ��4a��������1��x2��4����0��y2��5a������y2��y1�� ��x2��4����һԪ���η���cx2+bx+a=0��������Ϊ��1��![]() ������ȷ���۵�����ǣ� ��
������ȷ���۵�����ǣ� ��
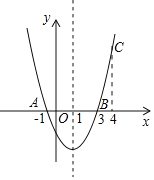
A.�٢�B.�٢�C.�ڢ�D.�٢ۢ�
���𰸡�A
��������
����A��B����д�������ߵĽ���ʽ�����![]() ������ɶ���ʽ
������ɶ���ʽ![]() �������жϢ٣���x=4ʱ��y=5a�����ݶ��κ��������ʣ������жϢڣ����ö��κ����ĶԳ��Լ������Լ����жϢۣ���
�������жϢ٣���x=4ʱ��y=5a�����ݶ��κ��������ʣ������жϢڣ����ö��κ����ĶԳ��Լ������Լ����жϢۣ���![]() ��֪b=��2a��c=��3a����cx2+bx+a=0�ɻ�Ϊ��3a x2��2a x+a=0��a��0���ⷽ�̼����жϢܣ�
��֪b=��2a��c=��3a����cx2+bx+a=0�ɻ�Ϊ��3a x2��2a x+a=0��a��0���ⷽ�̼����жϢܣ�
�⣺�����߽���ʽ���ɽ���ʽΪ![]() ��
��
��![]() ��
��
��ɶ���ʽ��![]() ��
��
�൱x=1ʱ�����κ�������СֵΪ��4a�����Ԣ���ȷ��
��x=4ʱ��![]() ��
��
�൱��1��x2��4����4a��y2��5a�����Ԣڴ���
��C�������Ϊ��4��5a����C�����ֱ��x=1�ĶԳƵ�Ϊ����2��5a����
����y2��y1���� x2��4��x2����2�����Ԣ۴���
��![]() ��֪b=��2a��c=��3a����cx2+bx+a=0�ɻ�Ϊ��3a x2��2a x+a=0��
��֪b=��2a��c=��3a����cx2+bx+a=0�ɻ�Ϊ��3a x2��2a x+a=0��
��a��0��
��̣�3a x2��2a x+a=0�����ã� 3a x2+2a x��a=0��
���![]() ��
��![]() ��
��
���Ԣ���ȷ��
���Ԣ٢���ȷ��
�ʴ�ѡ��A��


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD���ĸ��������۵���ƽ��ǡ��ƴ��һ����϶���ص��ľ���EFGH����EH��5��EF��12�������ABCD������ǣ� ��
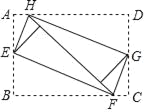
A. 13 B. ![]() C. 60 D. 120
C. 60 D. 120
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
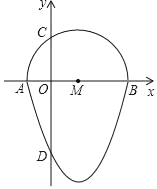
����Ŀ����ͼ�����ǰ�һ����Բ�������ߵ�һ����Χ�ɵķ��ͼ�γ�Ϊ����Բ������֪��A��B��C��D�ֱ��ǡ���Բ����������Ľ��㣬�����ߵĽ���ʽΪy=x2��6x��16��ABΪ��Բ��ֱ�������������Բ����y��صõ��߶�CD�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
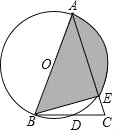
����Ŀ����ͼ������ABC�У�AB��AC��E��AC�ϣ�����A��B��E�����ԲO��BC�ڵ�D����D���ǻ�BE���е㣬
��1����֤AB��Բ��ֱ����
��2����AB��8����C��60��������Ӱ���ֵ������
��3������AΪ���ʱ����˵����A���CBE�Ĺ�ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ��������һ��ˮ���ijɱ�����![]() Ԫ/ǧ�ˣ������۹����з��֣�������ˮ���ļ۸���
Ԫ/ǧ�ˣ������۹����з��֣�������ˮ���ļ۸���![]() Ԫ/ǧ��ʱ��ÿ���������
Ԫ/ǧ��ʱ��ÿ���������![]() ǧ�ˣ��ڴ˻����ϣ�����ˮ���ĵ���ÿ���
ǧ�ˣ��ڴ˻����ϣ�����ˮ���ĵ���ÿ���![]() Ԫ/ǧ�ˣ���ˮ����ÿ��ͻ�������
Ԫ/ǧ�ˣ���ˮ����ÿ��ͻ�������![]() ǧ�ˣ�
ǧ�ˣ�
![]() ����ˮ����ÿ����������ˮ������õ�������
����ˮ����ÿ����������ˮ������õ�������![]() Ԫ����Ӧ��Ϊ���٣�
Ԫ����Ӧ��Ϊ���٣�
![]() �����������£�Ϊ�������ڹ˿ͣ�����Ӧ��Ϊ���٣�
�����������£�Ϊ�������ڹ˿ͣ�����Ӧ��Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ���ľߣ�����Ϊ5Ԫ/�����ۼ�Ϊ6Ԫ/��ʱ�������������Ϊ100���������۹����з��֣��ۼ�ÿ����0.5Ԫ��������������ͼ���5�����赱�����۵���ͳһΪ![]() Ԫ/����
Ԫ/����![]() ����
����![]() �ǰ�0.5Ԫ�ı������ǣ���������������Ϊ
�ǰ�0.5Ԫ�ı������ǣ���������������Ϊ![]() Ԫ��
Ԫ��
��1����![]() ��
��![]() �ĺ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ����
�ĺ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ����
��2��Ҫʹ��������������240Ԫ���������۵������ڵķ�Χ��
��3����ÿ���ľߵ�������![]() ��Ҫ�뵱�����������ÿ���ľ��ۼ�Ϊ����Ԫ��������������
��Ҫ�뵱�����������ÿ���ľ��ۼ�Ϊ����Ԫ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������Rt��ABC�У�BA=BC����ABC=90�㣬��D��AC�ϣ�����ABD�Ƶ�B��˳ʱ�뷽����ת90��õ���CBE��
��1�����DCE�Ķ�����
��2����AB=4��CD=3AD����DE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ�����κ���![]() ��ͼ��A��3��3������x�������ύ��B�㣬��y�ύ��C�㣬��ABC�����Բǡ�þ���ԭ��O.
��ͼ��A��3��3������x�������ύ��B�㣬��y�ύ��C�㣬��ABC�����Բǡ�þ���ԭ��O.
��1����B������꼰���κ����Ľ���ʽ��
��2����������һ��Q��m��m+3������mΪ����������MΪ��ABC�����Բ��һ���㣬���߶�QM���ȵķ�Χ��
��3������AOC��ƽ����һ��P��ת180������A'O'C'����O'��OΪ��Ӧ�㣩��ʹ�ø������εĶ�Ӧ���е�����������![]() ��ͼ���ϣ������ת����P������.
��ͼ���ϣ������ת����P������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����������ε����߳������㷽��x2-6x+8=0����������ε��ܳ�Ϊ______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com