
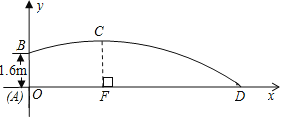
【题目】“阳光体育活动”促进了学校体育活动的开展,小杰在一次铅球比赛中,铅球出手以后的轨迹是抛物线的一部分(如图所示),已知铅球出手时离地面1.6米,铅球离投掷点3米时达到最高点,在离投掷点8米处落地,
(1)请求出此轨迹所在抛物线的关系式.
(2)设抛物线与X轴另一个交点是E,点Q是对称轴上的一个动点,求当△EBQ的周长最短时点Q的坐标.
(3)在抛物线上是否存在点G使得S△DEG=19.5,若存在请求出点G的坐标,若不存在,请说明理由.
【答案】(1)y=﹣0.1(x﹣3)2+2.5;(2)当△EBQ的周长最短时点Q的坐标为(3,1);(3)抛物线上是存在点G使得S△DEG=19.5,点G的坐标为(﹣5,﹣3.9),(11,﹣3.9).
【解析】
(1)根据题意得出抛物线顶点的横坐标为3,故设出抛物线的顶点式,再代入B、D的坐标可求出二次函数的解析式;
(2)E和D是关于对称轴的对称点,连接BD与CF的交点为Q,这时△EBQ的周长最短;求出直线BD的解析式,再求出它与对称轴的交点坐标即可;
(3)先假设存在,看能否求出符合条件的点G即可.
(1)根据题意,得
B(0,1.6),D(8,0),CF=3,
设抛物线解析式为y=a(x﹣3)2+h,
将B、D两点代入,得
![]() 解得
解得![]()
所以抛物线解析式为y=﹣0.1![]() +2.5.
+2.5.
(2)∵B(0,1.6),D(8,0)
∴直线BD:y=﹣0.2x+1.6.
令y=0即0=﹣0.1(x﹣3)2+2.5解得x1=8,x2=﹣2,
∴E(﹣2,0)
∵对称轴直线x=3.
∴当x=3时,y=1∴Q(3,1).
答:当△EBQ的周长最短时点Q的坐标为(3,1).
(3)抛物线上是存在点G使得S△DEG=19.5.理由如下:
设D点的纵坐标为y,∵S△DEG=19.5,即![]() ×10×|y|=19.5
×10×|y|=19.5
解得y=±3.9.
当y=3.9时,x无实数根,
当y=﹣3.9时,x1=11,x2=﹣5.
∴G(﹣5,﹣3.9),G(11,﹣3.9).
答:抛物线上是存在点G使得S△DEG=19.5,点G的坐标为(﹣5,﹣3.9),(11,﹣3.9).


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,点P是半径OB上一动点(不与O,B重合),过点P作射线l⊥AB,分别交弦BC,![]() 于D、E两点,在射线l上取点F,使FC=FD.
于D、E两点,在射线l上取点F,使FC=FD.
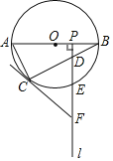
(1)求证:FC是⊙O的切线;
(2)当点E是![]() 的中点时,
的中点时,
① 若∠BAC=60°,判断以O,B,E,C为顶点的四边形是什么特殊四边形,并说明理由;
② 若![]() ,且AB=20,求OP的长.
,且AB=20,求OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“世界华人炎帝故里寻根节”,某工厂接到一批纪念品生产订单,按要求在15天内完成,约定这批纪念品的出厂价为每件20元,设第x天(1≤x≤15,且x为整数)每件产品的成本是p元,p与x之间符合一次函数关系,部分数据如表:
天数(x) | 1 | 3 | 6 | 10 |
每件成本p(元) | 7.5 | 8.5 | 10 | 12 |
任务完成后,统计发现工人李师傅第x天生产的产品件数y(件)与x(天)满足如下关系:y=![]() ,
,
设李师傅第x天创造的产品利润为W元.
(1)直接写出p与x,W与x之间的函数关系式,并注明自变量x的取值范围:
(2)求李师傅第几天创造的利润最大?最大利润是多少元?
(3)任务完成后.统计发现平均每个工人每天创造的利润为299元.工厂制定如下奖励制度:如果一个工人某天创造的利润超过该平均值,则该工人当天可获得20元奖金.请计算李师傅共可获得多少元奖金?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx(k≠0)经过点(12,﹣5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点),则m的取值范围为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
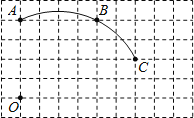
【题目】如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
(1)请完成如下操作:
①以点O为原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连结AD、CD
(2)请在(1)的基础上,完成下列填空:
①写出点的坐标:C______、D______.
②⊙D的半径=______(结果保留根号)
③求出弧AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象记为
的图象记为![]() ,它与x轴交于点O,
,它与x轴交于点O,![]() ;将
;将![]() 绕点
绕点![]() 旋转
旋转![]() 得
得![]() ,交x轴于点
,交x轴于点![]() ;将
;将![]() 绕点
绕点![]() 旋转
旋转![]() 得
得![]() ,交x轴于点
,交x轴于点![]() ;……如此进行下去,得到一条“波浪线”.若
;……如此进行下去,得到一条“波浪线”.若![]() 在这条“波浪线”上,则
在这条“波浪线”上,则![]() ________.
________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于O.点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于E,F两点,且∠MAN=45°,则下列结论:①MN=BM+DN;②△AEF∽△BEM;③![]() ;④△FMC是等腰三角形.其中正确的有( )
;④△FMC是等腰三角形.其中正确的有( )
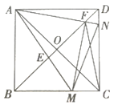
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com