
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,点P是半径OB上一动点(不与O,B重合),过点P作射线l⊥AB,分别交弦BC,![]() 于D、E两点,在射线l上取点F,使FC=FD.
于D、E两点,在射线l上取点F,使FC=FD.
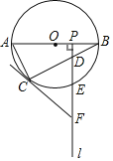
(1)求证:FC是⊙O的切线;
(2)当点E是![]() 的中点时,
的中点时,
① 若∠BAC=60°,判断以O,B,E,C为顶点的四边形是什么特殊四边形,并说明理由;
② 若![]() ,且AB=20,求OP的长.
,且AB=20,求OP的长.
【答案】(1)见解析;(2)①以O,B,E,C为顶点的四边形是菱形.理由见解析,②6.
【解析】
(1)连接OC,根据等边对等角及∠OBC+∠BDP=90°,证明∠OCB+∠FCD=90°即可;
(2)①四边形BOCE是菱形,证明△BOE,△OCE均为等边三角形,得到四条边相等,进而证明四边形BOCE是菱形;
②由![]() ,可求得AC=12,BC=16,由垂径定理可求出BH;利用三角形面积的不同表示方法求得PE=8,再利用勾股定理可求出OP的长.
,可求得AC=12,BC=16,由垂径定理可求出BH;利用三角形面积的不同表示方法求得PE=8,再利用勾股定理可求出OP的长.
解:(1)证明:连接OC,
∵OB=OC,
∴∠OBC=∠OCB,
∵PF⊥AB,
∴∠BPD=90°,
∴∠OBC+∠BDP=90°,
∵FC=FD
∴∠FCD=∠FDC
∵∠FDC=∠BDP
∴∠OCB+∠FCD=90°
∴OC⊥FC
∴FC是⊙O的切线;
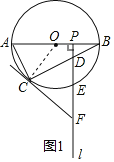
(2)如图2,连接OC,OE,BE,CE,
①以O,B,E,C为顶点的四边形是菱形.
理由如下:
∵AB是直径,∴∠ACB=90°,
∵∠BAC=60°,∴∠BOC=120°,
∵点E是![]() 的中点,
的中点,
∴∠BOE=∠COE=60°,
∵OB=OE=OC,
∴△BOE,△OCE均为等边三角形,
∴OB=BE=CE=OC,
∴四边形BOCE是菱形;
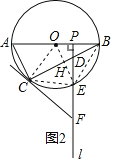
②∵![]() ,设AC=3k,BC=4k(k>0),
,设AC=3k,BC=4k(k>0),
由勾股定理得AC2+BC2=AB2,即(3k)2+(4k)2=202,解得k=4,
∴AC=12,BC=16,
∵点E是![]() 的中点,
的中点,
∴OE⊥BC,BH=CH=8,
∴![]() OE×BH=
OE×BH=![]() OB×PE,即10×8=10PE,解得:PE=8,
OB×PE,即10×8=10PE,解得:PE=8,
由勾股定理得OP=![]() =
=![]() =6.
=6.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】在“双11”期间,新华商场销售某种冰箱,每台进价为3000元,调查发现,当销售价为3600元时,平均每天能售出16台,而当销售价每降低50元时,平均每天就能多售出4台. 假设每台冰箱降价![]() 元(x为50的整数倍,0<x<600).
元(x为50的整数倍,0<x<600).
(1)直接写出平均每天商场销售冰箱的数量y(台)与x(元)之间的关系;
(2)要想这种冰箱的销售利润平均每天达到12800元,每台冰箱的定价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
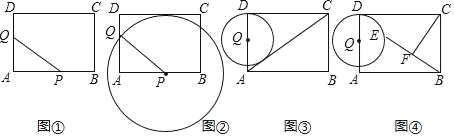
【题目】在矩形ABCD中,AB=8cm,BC=6cm,点P从点A出发,沿AB边向点B以每秒2cm的速度移动,同时点Q从点D出发沿DA边向点A以每秒1cm的速度移动,P、Q其中一点到达终点时,另一点随之停止运动.设运动时间为t秒.回答下列问题:
(1)如图①,几秒后△APQ的面积等于5cm2.
(2)如图②,若以点P为圆心,PQ为半径作⊙P.在运动过程中,是否存在t值,使得点C落在⊙P上?若存在,求出t的值;若不存在,请说明理由.
(3)如图③,若以Q为圆心,DQ为半径作⊙Q,当⊙Q与AC相切时
①求t的值.
②如图④,若点E是此时⊙Q上一动点,F是BE的中点,请直接写出CF的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]()
![]() 对称轴为______,顶点坐标为______;
对称轴为______,顶点坐标为______;
![]() 在坐标系中利用五点法画出此抛物线.
在坐标系中利用五点法画出此抛物线.
x |
| ______ | ______ | ______ | ______ | ______ |
|
y |
| ______ | ______ | ______ | ______ | ______ |
|
![]() 若抛物线与x轴交点为A、B,点
若抛物线与x轴交点为A、B,点![]() 在抛物线上,求
在抛物线上,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.

(1)求证:EF=MF;
(2)若AE=2,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:为解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可以将x2﹣1视为一个整体,然后设x2﹣1=y,则(x2﹣1)2=y2,原方程化为y2﹣5y+4=0.
解得y1=1,y2=4
当y=1时,x2﹣1=1.∴x2=2.∴x=±![]() ;
;
当y=4时,x2﹣1=4,∴x2=5,∴x=±![]() .
.
∴原方程的解为x1=![]() ,x2=﹣
,x2=﹣![]() ,x3=
,x3=![]() ,x4=﹣
,x4=﹣![]() ,
,
请利用以上知识解决下列问题:
如果(m2+n2﹣1)(m2+n2+2)=4,则m2+n2=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,如果AD=2cm,DB=1cm,AE=1.8cm,则EC=( )
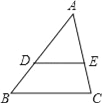
A. 0.9cm B. 1cm C. 3.6cm D. 0.2cm
【答案】A
【解析】试题分析:根据平行线分线段成比例定理得到![]() =
=![]() ,然后利用比例性质求EC的长.
,然后利用比例性质求EC的长.
解:∵DE∥BC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴EC=0.9(cm).
故选A.
考点:平行线分线段成比例.
【题型】单选题
【结束】
6
【题目】点C是线段AB的黄金分割点(AC>BC),若AB=10cm,则AC等于( )
A. 6 cm B. ![]() cm C.
cm C. ![]() cm D.
cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
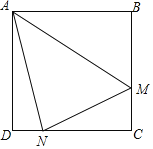
【题目】如图,在正方形![]() 中,点
中,点![]() 、
、![]() 为边
为边![]() 和
和![]() 上的动点(不含端点),
上的动点(不含端点),![]() .下列三个结论:①当
.下列三个结论:①当![]() 时,则
时,则![]() ;②
;②![]() ;③
;③![]() 的周长不变,其中正确结论的个数是( )
的周长不变,其中正确结论的个数是( )
A.0B.1
C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
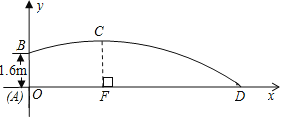
【题目】“阳光体育活动”促进了学校体育活动的开展,小杰在一次铅球比赛中,铅球出手以后的轨迹是抛物线的一部分(如图所示),已知铅球出手时离地面1.6米,铅球离投掷点3米时达到最高点,在离投掷点8米处落地,
(1)请求出此轨迹所在抛物线的关系式.
(2)设抛物线与X轴另一个交点是E,点Q是对称轴上的一个动点,求当△EBQ的周长最短时点Q的坐标.
(3)在抛物线上是否存在点G使得S△DEG=19.5,若存在请求出点G的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com