
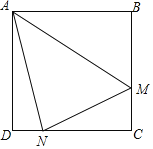
【题目】如图,在正方形![]() 中,点
中,点![]() 、
、![]() 为边
为边![]() 和
和![]() 上的动点(不含端点),
上的动点(不含端点),![]() .下列三个结论:①当
.下列三个结论:①当![]() 时,则
时,则![]() ;②
;②![]() ;③
;③![]() 的周长不变,其中正确结论的个数是( )
的周长不变,其中正确结论的个数是( )
A.0B.1
C.2D.3
【答案】D
【解析】
根据题目条件判定△AND≌△AMB,从而判断①的正误;利用截长补短的方法判定三角形全等,从而判断②③正误.
解:在正方形ABCD中,AD=AB=CD=CB,∠D=∠B=∠C=90°
∵![]()
∴![]()
∴∠NMC=45°,△MNC是等腰直角三角形
∴NC=MC
∴DN=BM
所以△AND≌△AMB
∴![]() ,因此①正确;
,因此①正确;
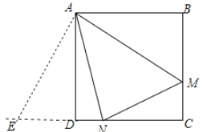
如图:延长CD,使得DE=BM
在△ADE和△ABM中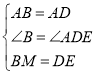
∴△ADE≌△ABM
∴![]() ,AM=AE
,AM=AE
∵![]()
∴![]()
∴![]()
∴![]()
又∵AE=AM,AN=AN
∴△AEN≌△AMN
∴MN=EN=ED+DN=BM+DN
∠AMN=∠E,∠ANM=∠ANE
∴∠ENM=∠ANM+∠ANE=2(180°-45°-∠AMN)=270°-2∠AMN
而∠MNC=180°-∠ENM=180°-(270°-2∠AMN)=2∠AMN-90°
即②![]() ,正确;
,正确;
![]() 的周长=MN+MC+NC=EN+NC+MC=ED+DN+NC+MC=BM+DN+NC+MC=CD+BC,即正方形边长的2倍,∴③
的周长=MN+MC+NC=EN+NC+MC=ED+DN+NC+MC=BM+DN+NC+MC=CD+BC,即正方形边长的2倍,∴③![]() 的周长不变,正确
的周长不变,正确
正确的共三个,故选:D.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣2x+c的顶点A在直线l:y=x﹣a上,点D(3,0)为抛物线上一点.
(1)求a的值;
(2)抛物线与y轴交于点B,试判断△ABD的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,点P是半径OB上一动点(不与O,B重合),过点P作射线l⊥AB,分别交弦BC,![]() 于D、E两点,在射线l上取点F,使FC=FD.
于D、E两点,在射线l上取点F,使FC=FD.
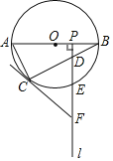
(1)求证:FC是⊙O的切线;
(2)当点E是![]() 的中点时,
的中点时,
① 若∠BAC=60°,判断以O,B,E,C为顶点的四边形是什么特殊四边形,并说明理由;
② 若![]() ,且AB=20,求OP的长.
,且AB=20,求OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知![]() ,
,![]() ,点
,点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动;点
的速度移动;点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.如果
的速度移动.如果![]() 、
、![]() 同时出发,用
同时出发,用![]() 表示移动的时间
表示移动的时间![]() ,
,
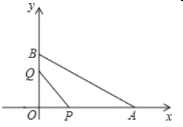
(1)用含![]() 的代数式表示:线段
的代数式表示:线段![]() ______;
______;![]() _______;
_______;![]() _______.
_______.
(2)当![]() 与
与![]() 相似时,求出
相似时,求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形![]() ,点
,点![]() 是其内部一点.
是其内部一点.

(1)如图1,点![]() 在边
在边![]() 的垂直平分线
的垂直平分线![]() 上,将
上,将![]() 绕点
绕点![]() 逆时针旋转,得到
逆时针旋转,得到![]() ,当点
,当点![]() 落在
落在![]() 上时,恰好点
上时,恰好点![]() 落在直线
落在直线![]() 上,求
上,求![]() 的度数;
的度数;
(2)如图2,点![]() 在对角线
在对角线![]() 上,连接
上,连接![]() ,若将线段
,若将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到线段
后得到线段![]() ,试问点
,试问点![]() 是否在直线
是否在直线![]() 上,请给出结论,并说明理由;
上,请给出结论,并说明理由;
(3)如图3,若![]() ,设
,设![]() ,
,![]() ,
,![]() ,请写出
,请写出![]() 、
、![]() 、
、![]() 这三条线段长之间满足的数量关系是____________.
这三条线段长之间满足的数量关系是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“世界华人炎帝故里寻根节”,某工厂接到一批纪念品生产订单,按要求在15天内完成,约定这批纪念品的出厂价为每件20元,设第x天(1≤x≤15,且x为整数)每件产品的成本是p元,p与x之间符合一次函数关系,部分数据如表:
天数(x) | 1 | 3 | 6 | 10 |
每件成本p(元) | 7.5 | 8.5 | 10 | 12 |
任务完成后,统计发现工人李师傅第x天生产的产品件数y(件)与x(天)满足如下关系:y=![]() ,
,
设李师傅第x天创造的产品利润为W元.
(1)直接写出p与x,W与x之间的函数关系式,并注明自变量x的取值范围:
(2)求李师傅第几天创造的利润最大?最大利润是多少元?
(3)任务完成后.统计发现平均每个工人每天创造的利润为299元.工厂制定如下奖励制度:如果一个工人某天创造的利润超过该平均值,则该工人当天可获得20元奖金.请计算李师傅共可获得多少元奖金?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx(k≠0)经过点(12,﹣5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点),则m的取值范围为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com