
【题目】在平面直角坐标系中,已知![]() ,
,![]() ,点
,点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动;点
的速度移动;点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动.如果
的速度移动.如果![]() 、
、![]() 同时出发,用
同时出发,用![]() 表示移动的时间
表示移动的时间![]() ,
,
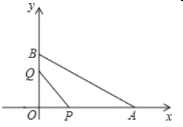
(1)用含![]() 的代数式表示:线段
的代数式表示:线段![]() ______;
______;![]() _______;
_______;![]() _______.
_______.
(2)当![]() 与
与![]() 相似时,求出
相似时,求出![]() 的值.
的值.
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】为倡导节能环保,降低能源消耗,提倡环保型新能源开发,造福社会.某公司研发生产一种新型智能环保节能灯,成本为每件40元.市场调查发现,该智能环保节能灯每件售价y(元)与每天的销售量为x(件)的关系如图,为推广新产品,公司要求每天的销售量不少于1000件,每件利润不低于5元.
(1)求每件销售单价y(元)与每天的销售量为x(件)的函数关系式并直接写出自变量x的取值范围;
(2)设该公司日销售利润为P元,求每天的最大销售利润是多少元?
(3)在试销售过程中,受国家政策扶持,毎销售一件该智能环保节能灯国家给予公司补贴m(m≤40)元.在获得国家每件m元补贴后,公司的日销售利润随日销售量的增大而增大,则m的取值范围是 (直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.

(1)求证:EF=MF;
(2)若AE=2,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,如果AD=2cm,DB=1cm,AE=1.8cm,则EC=( )
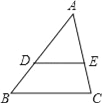
A. 0.9cm B. 1cm C. 3.6cm D. 0.2cm
【答案】A
【解析】试题分析:根据平行线分线段成比例定理得到![]() =
=![]() ,然后利用比例性质求EC的长.
,然后利用比例性质求EC的长.
解:∵DE∥BC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴EC=0.9(cm).
故选A.
考点:平行线分线段成比例.
【题型】单选题
【结束】
6
【题目】点C是线段AB的黄金分割点(AC>BC),若AB=10cm,则AC等于( )
A. 6 cm B. ![]() cm C.
cm C. ![]() cm D.
cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
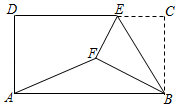
【题目】如图,在矩形ABCD中,AB=4,BC=![]() ,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=
,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=![]() ,则CE=_____.
,则CE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
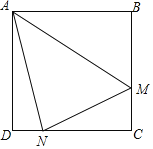
【题目】如图,在正方形![]() 中,点
中,点![]() 、
、![]() 为边
为边![]() 和
和![]() 上的动点(不含端点),
上的动点(不含端点),![]() .下列三个结论:①当
.下列三个结论:①当![]() 时,则
时,则![]() ;②
;②![]() ;③
;③![]() 的周长不变,其中正确结论的个数是( )
的周长不变,其中正确结论的个数是( )
A.0B.1
C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()

A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
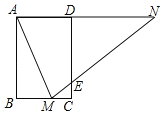
【题目】如图,矩形ABCD中,AB=3,BC=2,点M在BC上,连接AM,作∠AMN=∠AMB,点N在直线AD上,MN交CD于点E.
(1)求证:△AMN是等腰三角形;
(2)求证:AM2=2BMAN;
(3)当M为BC中点时,求ME的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=-![]() x2+
x2+![]() x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C:连接BC,点P为线段BC上方抛物线上的一动点,连接OP交BC于点Q.
x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C:连接BC,点P为线段BC上方抛物线上的一动点,连接OP交BC于点Q.
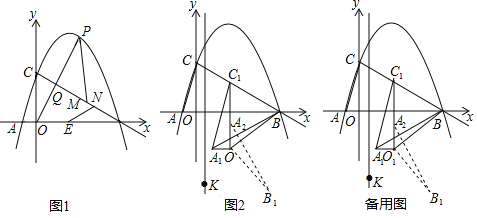
(1)如图1,当![]() 值最大时,点E为线段AB上一点,在线段BC上有两动点M,N(M在N上方),且MN=1,求PM+MN+NE-
值最大时,点E为线段AB上一点,在线段BC上有两动点M,N(M在N上方),且MN=1,求PM+MN+NE-![]() BE的最小值;
BE的最小值;
(2)如图2,连接AC,将△AOC沿射线CB方向平移,点A,C,O平移后的对应点分别记作A1,C1,O1,当C1B=O1B时,连接A1B、O1B,将△A1O1B绕点O1沿顺时针方向旋转90°后得△A2O1B1在直线x=![]() 上是否存在点K,使得△A2B1K为等腰三角形?若存在,直接写出点K的坐标;不存在,请说明理由.
上是否存在点K,使得△A2B1K为等腰三角形?若存在,直接写出点K的坐标;不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com