
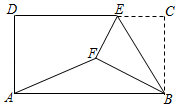
【题目】如图,在矩形ABCD中,AB=4,BC=![]() ,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=
,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=![]() ,则CE=_____.
,则CE=_____.
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
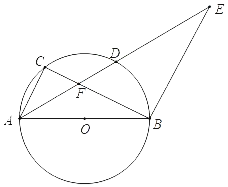
【题目】如图,AB是⊙O的直径,点C是圆上一点,点D是![]() 的中点,延长AD至点E,使得AB=BE.
的中点,延长AD至点E,使得AB=BE.
(1)求证:△ACF∽△EBF;
(2)若BE=10,tanE=![]() ,求CF的长.
,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
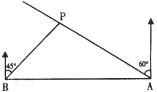
【题目】如图,在一笔直的海岸线上有A,B两个观测站,A在B的正东方向,有一艘小船停在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,BP=6![]() km.
km.
(1)求A、B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向前行,求观测站B与小船的最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若数a使关于x的不等式组 至少有3个整数解,且使关于y的分式方程
至少有3个整数解,且使关于y的分式方程![]() =2有非负整数解,则满足条件的所有整数a的和是( )
=2有非负整数解,则满足条件的所有整数a的和是( )
A. 14B. 15C. 23D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物y=﹣![]() 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.C,D两点关于抛物线对称轴对称,连接BD交y轴于点E,抛物线对称轴交x轴于点F.
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.C,D两点关于抛物线对称轴对称,连接BD交y轴于点E,抛物线对称轴交x轴于点F.
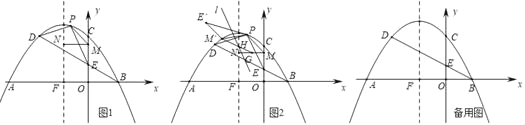
(1)点P为线段BD上方抛物线上的一点,连接PD,PE.点M是y轴上一点,过点M作MN⊥y轴交抛物线对称轴于点N.当△PDE面积最大时,求PM+MN+![]() NF的最小值;
NF的最小值;
(2)如图2,在(1)中PM+MN+![]() NF取得最小值时,将△PME绕点P顺时针旋转120°后得到△PM′E′,点G是MN的中点,连接M′G交抛物线的对称轴于点H,过点H作直线l∥PM,点R是直线l上一点,在平面直角坐标系中是否存在一点S,使以点M′,点G,点R,点S为顶点的四边形是矩形?若存在,直接写出点S的坐标,若不存在,请说明理由.
NF取得最小值时,将△PME绕点P顺时针旋转120°后得到△PM′E′,点G是MN的中点,连接M′G交抛物线的对称轴于点H,过点H作直线l∥PM,点R是直线l上一点,在平面直角坐标系中是否存在一点S,使以点M′,点G,点R,点S为顶点的四边形是矩形?若存在,直接写出点S的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,CB⊥AB,D为圆上一点,且AD∥OC,连接CD,AC,BD,AC与BD交于点M.
(1)求证:CD为⊙O的切线;
(2)若CD=![]() AD,求
AD,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件30元,售价为每件40元,每周可卖出180件;如果每件商品的售价每上涨1元,则每周就会少卖出5件,但每件售价不能高于55元,设每件商品的售价上涨x元(x为整数),每周的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)每件商品的售价为多少元时,每周可获得最大利润?最大利润是多少?
(3)每件商品的售价定为多少元时,每周的利润恰好是2145元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“扶贫攻坚”活动中,某单位计划选购甲、乙两种物品慰问贫困户.已知甲物品的单价比乙物品的单价高10元,若用500元单独购买甲物品与450元单独购买乙物品的数量相同.
①请问甲、乙两种物品的单价各为多少?
②如果该单位计划购买甲、乙两种物品共55件,总费用不少于5000元且不超过5050元,通过计算得出共有几种选购方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com