
ΓΨΧβΡΩΓΩ»γΆΦ≈ΉΈοyΘΫ©¹![]() ”κx÷αΫΜ”ΎAΘ§BΝΫΒψΘ®ΒψA‘ΎΒψBΒΡΉσ≤ύΘ©Θ§”κy÷αΫΜ”ΎΒψCΘ°CΘ§DΝΫΒψΙΊ”Ύ≈ΉΈοœΏΕ‘≥Τ÷αΕ‘≥ΤΘ§Ν§Ϋ”BDΫΜy÷α”ΎΒψEΘ§≈ΉΈοœΏΕ‘≥Τ÷αΫΜx÷α”ΎΒψFΘ°
”κx÷αΫΜ”ΎAΘ§BΝΫΒψΘ®ΒψA‘ΎΒψBΒΡΉσ≤ύΘ©Θ§”κy÷αΫΜ”ΎΒψCΘ°CΘ§DΝΫΒψΙΊ”Ύ≈ΉΈοœΏΕ‘≥Τ÷αΕ‘≥ΤΘ§Ν§Ϋ”BDΫΜy÷α”ΎΒψEΘ§≈ΉΈοœΏΕ‘≥Τ÷αΫΜx÷α”ΎΒψFΘ°
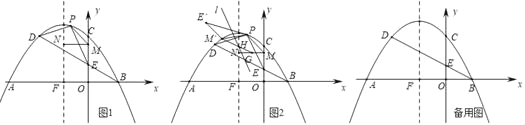
Θ®1Θ©ΒψPΈΣœΏΕΈBD…œΖΫ≈ΉΈοœΏ…œΒΡ“ΜΒψΘ§Ν§Ϋ”PDΘ§PEΘ°ΒψM «y÷α…œ“ΜΒψΘ§ΙΐΒψMΉςMNΓΆy÷αΫΜ≈ΉΈοœΏΕ‘≥Τ÷α”ΎΒψNΘ°Β±ΓςPDEΟφΜΐΉν¥σ ±Θ§«σPM+MN+![]() NFΒΡΉν–Γ÷ΒΘΜ
NFΒΡΉν–Γ÷ΒΘΜ
Θ®2Θ©»γΆΦ2Θ§‘ΎΘ®1Θ©÷–PM+MN+![]() NF»ΓΒΟΉν–Γ÷Β ±Θ§ΫΪΓςPME»ΤΒψPΥ≥ ±’κ–ΐΉΣ120ΓψΚσΒΟΒΫΓςPMΓδEΓδΘ§ΒψG «MNΒΡ÷–ΒψΘ§Ν§Ϋ”MΓδGΫΜ≈ΉΈοœΏΒΡΕ‘≥Τ÷α”ΎΒψHΘ§ΙΐΒψHΉς÷±œΏlΓΈPMΘ§ΒψR «÷±œΏl…œ“ΜΒψΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷– «Ζώ¥φ‘Ύ“ΜΒψSΘ§ Ι“‘ΒψMΓδΘ§ΒψGΘ§ΒψRΘ§ΒψSΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΨΊ–ΈΘΩ»τ¥φ‘ΎΘ§÷±Ϋ”–¥≥ωΒψSΒΡΉχ±ξΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
NF»ΓΒΟΉν–Γ÷Β ±Θ§ΫΪΓςPME»ΤΒψPΥ≥ ±’κ–ΐΉΣ120ΓψΚσΒΟΒΫΓςPMΓδEΓδΘ§ΒψG «MNΒΡ÷–ΒψΘ§Ν§Ϋ”MΓδGΫΜ≈ΉΈοœΏΒΡΕ‘≥Τ÷α”ΎΒψHΘ§ΙΐΒψHΉς÷±œΏlΓΈPMΘ§ΒψR «÷±œΏl…œ“ΜΒψΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷– «Ζώ¥φ‘Ύ“ΜΒψSΘ§ Ι“‘ΒψMΓδΘ§ΒψGΘ§ΒψRΘ§ΒψSΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΨΊ–ΈΘΩ»τ¥φ‘ΎΘ§÷±Ϋ”–¥≥ωΒψSΒΡΉχ±ξΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©PM+MN+![]() NFΒΡΉν–Γ÷ΒΘΫ
NFΒΡΉν–Γ÷ΒΘΫ![]() ΘΜΘ®2Θ©¥φ‘ΎΘ§ΒψSΒΡΉχ±ξΈΣΘΚS1Θ®
ΘΜΘ®2Θ©¥φ‘ΎΘ§ΒψSΒΡΉχ±ξΈΣΘΚS1Θ®![]() Θ§
Θ§![]() Θ©Θ§S2Θ®
Θ©Θ§S2Θ®![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©¥ΐΕ®œΒ ΐΖ®«σ÷±œΏBDΫβΈω ΫΘ§‘ΌΗυΨίΕΰ¥ΈΚ· ΐΉν¥σ÷ΒΖΫΖ®«σΓςPDEΟφΜΐΉν¥σ ±Ε‘”ΠΒΡΒψPΉχ±ξΘ§ΉνΚσ“άΨίΝΫΒψ÷°ΦδœΏΕΈΉνΕΧ«σPM+MN+![]() NFΒΡΉν–Γ÷ΒΘΜ
NFΒΡΉν–Γ÷ΒΘΜ
Θ®2Θ©”…–ΐΉΣ«σΒψMΓδΉχ±ξΘ§¥ΐΕ®œΒ ΐΖ®«σ÷±œΏPMΫβΈω ΫΓΔ÷±œΏMΓδG“‘ΦΑ÷±œΏlΒΡΫβΈω ΫΘ§“άΨίΨΊ–Έ–‘÷ Ζ÷άύΧ÷¬έ«σRΉχ±ξΘ§‘ΌΗυΨίΤΫ“ΤΙφ¬…«σœύ”ΠΒΡSΉχ±ξΘ°
Θ®1Θ©‘Ύ≈ΉΈοœΏyΘΫ©¹![]() x2-
x2-![]() ÷–Θ§ΝνxΘΫ0Θ§ΒΟΘΚyΘΫ
÷–Θ§ΝνxΘΫ0Θ§ΒΟΘΚyΘΫ![]() Θ§ΝνyΘΫ0Θ§ΒΟΘΚ
Θ§ΝνyΘΫ0Θ§ΒΟΘΚ
x1ΘΫ©¹3Θ§x2ΘΫ1
ΓύAΘ®©¹3Θ§0Θ©Θ§BΘ®1Θ§0Θ©Θ§CΘ®0Θ§![]() Θ©,
Θ©,
ΓΏyΘΫ©¹![]() x2
x2![]() ΘΫ
ΘΫ![]() Θ§
Θ§
Γύ≈ΉΈοœΏΕ‘≥Τ÷αΈΣΘΚ÷±œΏxΘΫ©¹1
ΓύDΘ®©¹2Θ§![]() Θ©Θ§
Θ©Θ§
…η÷±œΏBDΫβΈω ΫΈΣyΘΫkx+bΘ§ΫΪBΘ®1Θ§0Θ©Θ§DΘ®©¹2Θ§![]() Θ©¥ζ»κΒΟ
Θ©¥ζ»κΒΟ Θ§
Θ§
ΫβΒΟΘΚ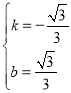
Γύ÷±œΏBDΫβΈω ΫΈΣyΘΫ-![]() x+
x+![]()
ΓύEΘ®0Θ§![]() Θ©Θ§
Θ©Θ§
ΙΐΒψPΉςPGΓΆx÷α”ΎGΫΜBD”ΎHΘ§ΉςPQΓΆBD”ΎQΘ§Ν§Ϋ”CDΘ§
…ηPΘ®mΘ§-![]() m2-
m2-![]() +
+![]() ȩȧHȮmȧ-
ȩȧHȮmȧ-![]() m+
m+![]() Θ©
Θ©
PHΘΫ-![]() m2-
m2-![]() +
+![]()
ΓΏPGΓΈy÷α
ΓύΓœPHDΘΫΓœDECΘ§
ΓΏCΓΔDΙΊ”Ύ÷±œΏxΘΫ©¹1Ε‘≥ΤΘ§
ΓύΓœDCEΘΫΓœPQEΘΫ90Γψ
ΓύΓςDCEΓΉΓςHQP
Γύ![]() Θ§Φ¥ΘΚPQDEΘΫDCPHΘ§
Θ§Φ¥ΘΚPQDEΘΫDCPHΘ§
ΓύSΓςPDEΘΫ![]() PQDEΘΫ
PQDEΘΫ![]() DCPHΘΫ
DCPHΘΫ![]() ΓΝ2Θ®-
ΓΝ2Θ®-![]() m2-
m2-![]() +
+![]() Θ©
Θ©
ΘΫ-![]() Θ§
Θ§
ΓΏ-![]() ΘΦ0,
ΘΦ0,
ΓύΒ±mΘΫ©¹![]() ±Θ§SΓςPDEΒΡΉν¥σ÷ΒΘΫ
±Θ§SΓςPDEΒΡΉν¥σ÷ΒΘΫ![]() Θ§¥Υ ±Θ§PΘ®©¹
Θ§¥Υ ±Θ§PΘ®©¹![]() Θ§
Θ§![]() Θ©Θ§
Θ©Θ§
ΙΐΒψFΉςΓœNFSΘΫ60ΓψΘ§ΙΐNΉςΓœFNSΘΫ30ΓψΘ§FS”κNSΫΜ”ΎΒψSΘ§»γΆΦΘ§
ΓύΓœFSNΘΫ90ΓψΘ§
ΓύNSΘΫNFcosΓœFNSΘΫNFcos30ΓψΘΫ![]() NFΘ§ΙΐMΉςMKΓΈNSΘ§«“MKΘΫNSΘ§
NFΘ§ΙΐMΉςMKΓΈNSΘ§«“MKΘΫNSΘ§
Β±PΓΔMΓΔK»ΐΒψΙ≤œΏ ±Θ§PM+MKΉν–ΓΘ§
ΓύΓœPMCΘΫΓœKMEΘΫΓœFNSΘΫ30Γψ
ΓύPMΘΫ2PLΘΫ1Θ§LMΘΫ![]() Θ§MKΘΫNSΘΫ
Θ§MKΘΫNSΘΫ![]() NFΘΫ
NFΘΫ![]() Θ®
Θ®![]() ©¹
©¹![]() Θ©ΘΫ
Θ©ΘΫ![]() Θ§MNΘΫ1
Θ§MNΘΫ1
ΓύPM+MN+![]() NFΒΡΉν–Γ÷ΒΘΫ1+1+
NFΒΡΉν–Γ÷ΒΘΫ1+1+![]() ΘΫ
ΘΫ![]() .
.

Θ®2Θ©»γΆΦ:
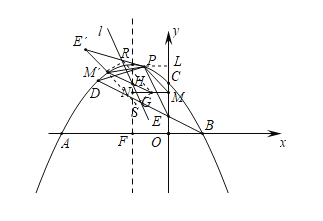
”…Θ®1Θ©÷ΣΘΚPΘ®©¹![]() Θ§
Θ§![]() Θ©Θ§MΘ®0Θ§
Θ©Θ§MΘ®0Θ§![]() Θ©Θ§Ω…«σΒΟ÷±œΏPMΫβΈω ΫΈΣΘΚyΘΫ-
Θ©Θ§Ω…«σΒΟ÷±œΏPMΫβΈω ΫΈΣΘΚyΘΫ-![]() x+
x+![]() Θ§
Θ§
ΓΏΓœPMLΘΫ30ΓψΘ§ΓœPLMΘΫ90ΓψΘ§ΓύΓœLPMΘΫ60Γψ
ΓΏΓœMPMΓδΘΫ120ΓψΘ§PMΓδΘΫPMΘΫ1
ΓύMΓδΓΔPΓΔL»ΐΒψΙ≤œΏΘ§ΓύMΓδΘ®-![]() Θ§
Θ§![]() Θ©Θ§
Θ©Θ§
ΓΏΒψG «MNΒΡ÷–ΒψΘ§
ΓύGΘ®-![]() Θ§
Θ§![]() Θ©Θ§¥ΐΕ®œΒ ΐΖ®Ω…«σΒΟ÷±œΏMΓδGΒΡΫβΈω ΫΈΣΘΚyΘΫ-
Θ©Θ§¥ΐΕ®œΒ ΐΖ®Ω…«σΒΟ÷±œΏMΓδGΒΡΫβΈω ΫΈΣΘΚyΘΫ-![]() Θ§ΝνxΘΫ©¹1Θ§ΒΟyΘΫ
Θ§ΝνxΘΫ©¹1Θ§ΒΟyΘΫ![]()
ΓύHΘ®©¹1Θ§![]() Θ©Θ§ΓΏ÷±œΏlΓΈPM«“ΙΐΒψHΘ§
Θ©Θ§ΓΏ÷±œΏlΓΈPM«“ΙΐΒψHΘ§
Γύ÷±œΏlΒΡΫβΈω ΫΈΣΘΚyΘΫ-![]() xΘ§…ηRΘ®tΘ§-
xΘ§…ηRΘ®tΘ§-![]() tΘ©Θ§ΓΏ“‘ΒψMΓδΘ§ΒψGΘ§ΒψRΘ§ΒψSΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΨΊ–Έ
tΘ©Θ§ΓΏ“‘ΒψMΓδΘ§ΒψGΘ§ΒψRΘ§ΒψSΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΨΊ–Έ
ΓύΩ…“‘Ζ÷ΝΫ÷÷«ι–ΈΘΚMΓδGΈΣ±ΏΜρMΓδGΈΣΕ‘Ϋ«œΏ
ΔΌMΓδGΈΣ±ΏΘ§ΓœRMΓδGΘΫ90Γψ ±
ΓύMΓδR2+MΓδH2ΘΫRH2Θ§Φ¥ΘΚ(t+ ΘΫΘ®t+1Θ©2+(-
ΘΫΘ®t+1Θ©2+(-![]() t-
t-![]() )2
)2
ΫβΒΟΘΚtΘΫ-![]() Θ§
Θ§
ΓύRΘ®©¹![]() Θ§
Θ§![]() Θ©Θ§”…ΤΫ“ΤΩ…ΒΟS1Θ®-
Θ©Θ§”…ΤΫ“ΤΩ…ΒΟS1Θ®-![]() Θ§
Θ§![]() Θ©Θ§
Θ©Θ§
ΔΎMΓδGΈΣ±ΏΘ§ΓœMΓδGRΘΫ90Γψ ±
ΓύGR2+HG2ΘΫHR2Θ§Φ¥ΘΚ(t+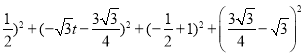 ΘΫΘ®t+1Θ©2+(-
ΘΫΘ®t+1Θ©2+(-![]() t-
t-![]() )2Θ§
)2Θ§
ΫβΒΟΘΚtΘΫ-![]() Θ§
Θ§
ΓύRΘ®-![]() Θ§
Θ§![]() Θ©Θ§”…ΤΫ“ΤΩ…ΒΟS2Θ®-
Θ©Θ§”…ΤΫ“ΤΩ…ΒΟS2Θ®-![]() Θ§
Θ§![]() Θ©,
Θ©,
ΔέMΓδGΈΣΕ‘Ϋ«œΏΘ§ΓœMΓδRGΘΫ90Γψ
ΓύMΓδR2+RG2ΘΫMΓδG2Θ§Φ¥ΘΚ(t+![]() )2+(-
)2+(-![]() -
-![]() )2+(t+
)2+(t+![]() )2+(-
)2+(-![]() ΘΫ(-
ΘΫ(-![]() Θ§ΈόΫβΘΜ
Θ§ΈόΫβΘΜ
Ήέ…œΥυ ωΘ§ΒψSΒΡΉχ±ξΈΣΘΚS1Θ®-![]() Θ©Θ§S2Θ®-
Θ©Θ§S2Θ®-![]() Θ©Θ°
Θ©Θ°


 Ϋρ«≈ΫΧ”ΐΦΤΥψ–ΓΉ¥‘ΣœΒΝ–¥πΑΗ
Ϋρ«≈ΫΧ”ΐΦΤΥψ–ΓΉ¥‘ΣœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ ΙΒΟΚ· ΐ÷ΒΈΣ0ΒΡΉ‘±δΝΩΒΡ÷Β≥ΤΈΣΚ· ΐΒΡΝψΒψΘ°άΐ»γΘ§Ε‘”ΎΚ· ΐy=x©¹1Θ§Ννy=0Ω…ΒΟx=1Θ§Έ“Ο«ΥΒ1 «Κ· ΐy=x©¹1ΒΡΝψΒψΘ°“―÷ΣΚ· ΐy=x2©¹2mx©¹2Θ®m+3Θ©Θ®mΈΣ≥Θ ΐΘ©
Θ®1Θ©Β±m=0 ±Θ§«σΗΟΚ· ΐΒΡΝψΒψΘ°
Θ®2Θ©÷ΛΟςΘΚΈό¬έm»ΓΚΈ÷ΒΘ§ΗΟΚ· ΐΉή”–ΝΫΗωΝψΒψΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
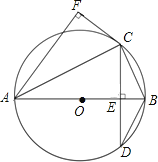
ΓΨΧβΡΩΓΩ»γΆΦΘ§ABΈΣΓ―OΒΡ÷±ΨΕΘ§œ“CDΓΆABΘ§¥ΙΉψΈΣΒψEΘ§CFΓΆAFΘ§«“CF=CEΘ°
Θ®1Θ©«σ÷ΛΘΚCF «Γ―OΒΡ«–œΏΘΜ
Θ®2Θ©»τsinΓœBAC=![]() Θ§«σ
Θ§«σ![]() ΒΡ÷ΒΘ°
ΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
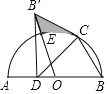
ΓΨΧβΡΩΓΩ»γΆΦΘ§“‘ABΈΣ÷±ΨΕΘ§ΒψOΈΣ‘≤–ΡΒΡΑκ‘≤…œ”–“ΜΒψCΘ§«“ΓœABCΘΫ60ΓψΘ§ΒψDΈΣAO…œ“ΜΒψΘ°ΫΪΓςDBC―Ί÷±œΏDCΕ‘’έΒΟΒΫΓςDB'CΘ§ΒψBΒΡΕ‘”ΠΒψΈΣBΓδΘ§«“B'C”κΑκ‘≤œύ«–”ΎΒψCΘ§Ν§Ϋ”BΓδOΫΜΑκ‘≤”ΎΒψEΘ°
Θ®1Θ©«σ÷ΛΘΚB'DΓΆABΘΜ
Θ®2Θ©Β±ABΘΫ2 ±Θ§«σΆΦ÷–“θ”Α≤ΩΖ÷ΟφΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
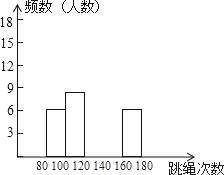
ΓΨΧβΡΩΓΩΈΣΝΥΫχ“Μ≤ΫΝΥΫβΑΥΡξΦΕ―ß…ζΒΡ…μΧεΥΊ÷ «ιΩωΘ§Χε”ΐάœ Π“‘ΑΥΡξΦΕΘ®1Θ©Αύ50ΈΜ―ß…ζΈΣ―υ±ΨΫχ––ΝΥ“ΜΖ÷÷”Χχ…ΰ¥Έ ΐ≤β ‘Θ°ΗυΨί≤β ‘ΫαΙϊΘ§Μφ÷Τ≥ω≤ΩΖ÷ΤΒ ΐΖ÷≤Φ±μΚΆ≤ΩΖ÷ΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘ°
Ήι±π | ¥Έ ΐx | ΤΒ ΐΘ®»Υ ΐΘ© |
ΒΎ1Ήι | 80ΓήxΘΦ100 | 6 |
ΒΎ2Ήι | 100ΓήxΘΦ120 | 8 |
ΒΎ3Ήι | 120ΓήxΘΦ140 | a |
ΒΎ4Ήι | 140ΓήxΘΦ160 | 18 |
ΒΎ5Ήι | 160ΓήxΘΦ180 | 6 |
«κΫαΚœΆΦ±μΆξ≥…œ¬Ν–Έ ΧβΘΚ
Θ®1Θ©±μ÷–ΒΡaΘΫΓΓ ΓΓΘΜ
Θ®2Θ©«κΑ―ΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦ≤Ι≥δΆξ’ϊΘΜ
Θ®3Θ©’βΗω―υ±Ψ ΐΨίΒΡ÷–ΈΜ ΐ¬δ‘ΎΒΎΓΓ ΓΓΉιΘΜ
Θ®4Θ©“―÷ΣΗΟ–ΘΑΥΡξΦΕΙ≤”–―ß…ζ800Θ§«κΡψΙάΦΤ“ΜΖ÷÷”Χχ…ΰ¥Έ ΐ≤ΜΒΆ”Ύ120¥ΈΒΡΑΥΡξΦΕ―ß…ζ¥σ‘ΦΕύ…ΌΟϊΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
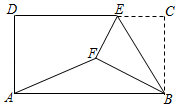
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΨΊ–ΈABCD÷–Θ§ABΘΫ4Θ§BCΘΫ![]() Θ§EΈΣCD±Ώ…œ“ΜΒψΘ§ΫΪΓςBCE―ΊBE’έΒΰΘ§ ΙΒΟC¬δΒΫΨΊ–ΈΡΎΒψFΒΡΈΜ÷ΟΘ§Ν§Ϋ”AFΘ§»τtanΓœBAFΘΫ
Θ§EΈΣCD±Ώ…œ“ΜΒψΘ§ΫΪΓςBCE―ΊBE’έΒΰΘ§ ΙΒΟC¬δΒΫΨΊ–ΈΡΎΒψFΒΡΈΜ÷ΟΘ§Ν§Ϋ”AFΘ§»τtanΓœBAFΘΫ![]() Θ§‘ρCEΘΫ_____Θ°
Θ§‘ρCEΘΫ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥÷–―ßΈΣΝΥ¥¥Ϋ®ΓΑΉνΟά–Θ‘ΑΆΦ ιΈίΓ±–¬ΙΚ¬ρΝΥ“Μ≈ζΆΦ ιΘ§Τδ÷–ΩΤΤ’άύΆΦ ιΤΫΨυΟΩ±ΨΒΡΦέΗώ «ΈΡ―ßάύΆΦ ιΤΫΨυΟΩ±Ψ ιΦέΗώΒΡ1.2±ΕΘ§“―÷Σ―ß–Θ”Ο12000‘ΣΙΚ¬ρΈΡ―ßάύΆΦ ιΒΡ±Ψ ΐ±»”Ο’β–©«°ΙΚ¬ρΩΤΤ’άύΆΦ ιΒΡ±Ψ ΐΕύ100±ΨΘ§Ρ«Ο¥―ß–ΘΙΚ¬ρΈΡ―ßάύΆΦ ιΤΫΨυΟΩ±Ψ ιΒΡΦέΗώ «Θ®ΓΓΓΓΘ©
A.20‘ΣB.18‘ΣC.15‘ΣD.10‘Σ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣ≈ύ―χ―ß…ζΒΡ¥¥‘λ–‘ΥΦΈ§,―ß–ΘΨΌ––ΩΤΦΦ–Γ÷ΤΉς±»»ϋΘ°Ε‘ΙΪΩΣ’ςΦ·ΒΫΒΡΩΤΦΦ–Γ÷ΤΉςΉςΤΖΒΡ ΐΝΩΫχ––ΝΥΖ÷ΈωΆ≥ΦΤ,≤Δ÷ΤΉςΝΥ»γœ¬Ά≥ΦΤΆΦΘ°
Θ®1Θ©―ß–ΘΙ≤’ςΦ·ΒΫΉςΤΖΙ≤ΓΓ ΓΓΦΰ;
Θ®2Θ©Ψ≠ΙΐΤά―ΓΚσ,”–2ΟϊΡ–…ζΚΆ2Οϊ≈°…ζΜώΒΟ“ΜΒ»Ϋ±Θ°œ÷“Σ¥”’β4ΈΜΆ§―ß÷–≥ιΝΫ»Υ»Ξ≤ΈΦ”±μ’ΟΉυΧΗΜα,«κ”Ο ςΉ¥ΆΦΜρΝ–±μΖ®«σ≥ω«ΓΚΟ≥ι÷–“ΜΡ–“Μ≈°ΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœACBΘΫ90ΓψΘ§ACΘΫBCΘΫ2Θ§ΫΪΓςABC»ΤACΒΡ÷–ΒψDΡφ ±’κ–ΐΉΣ90ΓψΒΟΒΫΓςAΓδBΓδCΓδΘ§Τδ÷–ΒψBΒΡ‘ΥΕ·¬ΖΨΕΈΣ![]() Θ§‘ρΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΈΣΘ®ΓΓΓΓΘ©
Θ§‘ρΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΈΣΘ®ΓΓΓΓΘ©
A.![]() Π–©¹
Π–©¹![]() B.2C.
B.2C.![]() D.
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com