
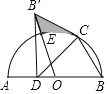
【题目】如图,以AB为直径,点O为圆心的半圆上有一点C,且∠ABC=60°,点D为AO上一点.将△DBC沿直线DC对折得到△DB'C,点B的对应点为B′,且B'C与半圆相切于点C,连接B′O交半圆于点E.
(1)求证:B'D⊥AB;
(2)当AB=2时,求图中阴影部分面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OC,根据切线的性质得到∠B'CO=90,根据等边三角形的性质、翻转变换的性质计算,得到∠B′DB=90°,证明结论;
(2)求出∠B′OC=45°,根据三角形的面积公式、扇形面积公式计算即可.
(1)证明:连接OC,
∵B'C与半圆相切于点C,
∴∠B'CO=90,
∵OC=OB,∠ABC=60°,
∴△OBC是等边三角形,
∴∠OCB=60°,∠B'CB=∠B'CO+∠OCB=90°+60°=150°,
∵△DBC沿直线DC对折得到△DB'C,
∴∠DCB=![]() ∠B’CB=
∠B’CB=![]() ×150°=75°,
×150°=75°,
在△DBC中,∠CDB=180°﹣∠ABC﹣∠DCB=180°﹣75°﹣60°=45°
∴∠B′DB=2∠CDB=2×45°=90°,
∴B′D⊥AB;
(2)解:∵AB=2,△OBC是等边三角形,
∴OC=OB=BC=B'C=1,
∵∠B'CO=90°,
∴∠B′OC=45°,
∴阴影部分的面积=S△B′OC﹣S扇形EOC=![]() B′CCO﹣
B′CCO﹣![]() =
=![]() ×1×1﹣
×1×1﹣![]() =
=![]() .
.



科目:初中数学 来源: 题型:
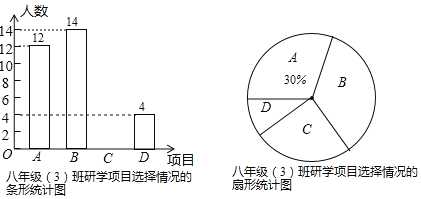
【题目】某学校开展以素质提升为主题的研学活动,推出了以下四个项目供学生选择:A.模拟驾驶;B.军事竞技;C.家乡导游;D.植物识别.学校规定:每个学生都必须报名且只能选择其中一个项目.八年级(3)班班主任刘老师对全班学生选择的项目情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
(1)八年级(3)班学生总人数是 ,并将条形统计图补充完整;
(2)刘老师发现报名参加“植物识别”的学生中恰好有两名男生,现准备从这些学生中任意挑选两名担任活动记录员,请用列表或画树状图的方法,求恰好选中1名男生和1名女生担任活动记录员的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知梯形![]() 中,
中,![]() ∥
∥![]() ,且
,且![]() ,
,![]() ,
,![]() 。
。
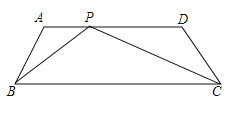
⑴如图,P为![]() 上的一点,满足∠BPC=∠A,求AP的长;
上的一点,满足∠BPC=∠A,求AP的长;
⑵如果点P在![]() 边上移动(点P与点
边上移动(点P与点![]() 不重合),且满足∠BPE=∠A,
不重合),且满足∠BPE=∠A,![]() 交直线
交直线![]() 于点E,同时交直线DC于点
于点E,同时交直线DC于点![]() 。
。
①当点![]() 在线段DC的延长线上时,设
在线段DC的延长线上时,设![]() ,CQ=y,求
,CQ=y,求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
②写CE=1时,写出AP的长(不必写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
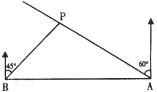
【题目】如图,在一笔直的海岸线上有A,B两个观测站,A在B的正东方向,有一艘小船停在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,BP=6![]() km.
km.
(1)求A、B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向前行,求观测站B与小船的最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
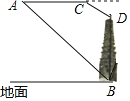
【题目】某兴趣小组同学借助无人机航拍测量某公园内一座古塔高度.如图,无人机在距离地面168米的A处,测得该塔底端点B的俯角为40°,然后向古塔方向沿水平面飞行50秒到达点C处,此时测得该塔顶端点D的俯角为60°.已知无人机的飞行速度为3米/秒,则这座古塔的高度约为_____米(参考计算:sin40°≈064.cos40°≈077.tan40°≈0.84.![]() ≈1.41.
≈1.41.![]() 1.73.结果精确到0.1米)
1.73.结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若数a使关于x的不等式组 至少有3个整数解,且使关于y的分式方程
至少有3个整数解,且使关于y的分式方程![]() =2有非负整数解,则满足条件的所有整数a的和是( )
=2有非负整数解,则满足条件的所有整数a的和是( )
A. 14B. 15C. 23D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物y=﹣![]() 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.C,D两点关于抛物线对称轴对称,连接BD交y轴于点E,抛物线对称轴交x轴于点F.
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.C,D两点关于抛物线对称轴对称,连接BD交y轴于点E,抛物线对称轴交x轴于点F.
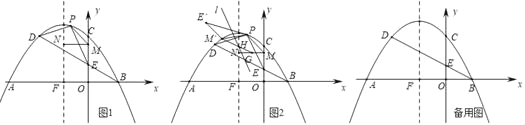
(1)点P为线段BD上方抛物线上的一点,连接PD,PE.点M是y轴上一点,过点M作MN⊥y轴交抛物线对称轴于点N.当△PDE面积最大时,求PM+MN+![]() NF的最小值;
NF的最小值;
(2)如图2,在(1)中PM+MN+![]() NF取得最小值时,将△PME绕点P顺时针旋转120°后得到△PM′E′,点G是MN的中点,连接M′G交抛物线的对称轴于点H,过点H作直线l∥PM,点R是直线l上一点,在平面直角坐标系中是否存在一点S,使以点M′,点G,点R,点S为顶点的四边形是矩形?若存在,直接写出点S的坐标,若不存在,请说明理由.
NF取得最小值时,将△PME绕点P顺时针旋转120°后得到△PM′E′,点G是MN的中点,连接M′G交抛物线的对称轴于点H,过点H作直线l∥PM,点R是直线l上一点,在平面直角坐标系中是否存在一点S,使以点M′,点G,点R,点S为顶点的四边形是矩形?若存在,直接写出点S的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件30元,售价为每件40元,每周可卖出180件;如果每件商品的售价每上涨1元,则每周就会少卖出5件,但每件售价不能高于55元,设每件商品的售价上涨x元(x为整数),每周的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)每件商品的售价为多少元时,每周可获得最大利润?最大利润是多少?
(3)每件商品的售价定为多少元时,每周的利润恰好是2145元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知B港口位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为16km,一艘货轮从B港口以40km/h的速度沿如图所示的BC方向航行,15min后达到C处,现测得C处位于A观测点北偏东79.8°方向,求此时货轮与A观测点之间的距离AC的长(精确到0.1km).(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,![]() ≈1.41,
≈1.41,![]() ≈2.24)
≈2.24)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com