
【题目】为培养学生的创造性思维,学校举行科技小制作比赛.对公开征集到的科技小制作作品的数量进行了分析统计,并制作了如下统计图.
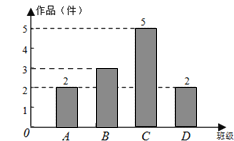
(1)学校共征集到作品共 件;
(2)经过评选后,有2名男生和2名女生获得一等奖.现要从这4位同学中抽两人去参加表彰座谈会,请用树状图或列表法求出恰好抽中一男一女的概率.
 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】已知梯形![]() 中,
中,![]() ∥
∥![]() ,且
,且![]() ,
,![]() ,
,![]() 。
。
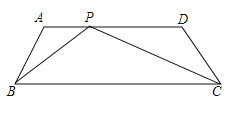
⑴如图,P为![]() 上的一点,满足∠BPC=∠A,求AP的长;
上的一点,满足∠BPC=∠A,求AP的长;
⑵如果点P在![]() 边上移动(点P与点
边上移动(点P与点![]() 不重合),且满足∠BPE=∠A,
不重合),且满足∠BPE=∠A,![]() 交直线
交直线![]() 于点E,同时交直线DC于点
于点E,同时交直线DC于点![]() 。
。
①当点![]() 在线段DC的延长线上时,设
在线段DC的延长线上时,设![]() ,CQ=y,求
,CQ=y,求![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
②写CE=1时,写出AP的长(不必写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物y=﹣![]() 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.C,D两点关于抛物线对称轴对称,连接BD交y轴于点E,抛物线对称轴交x轴于点F.
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.C,D两点关于抛物线对称轴对称,连接BD交y轴于点E,抛物线对称轴交x轴于点F.
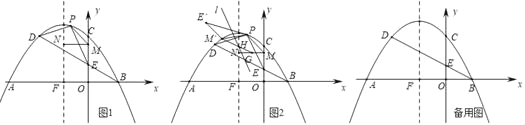
(1)点P为线段BD上方抛物线上的一点,连接PD,PE.点M是y轴上一点,过点M作MN⊥y轴交抛物线对称轴于点N.当△PDE面积最大时,求PM+MN+![]() NF的最小值;
NF的最小值;
(2)如图2,在(1)中PM+MN+![]() NF取得最小值时,将△PME绕点P顺时针旋转120°后得到△PM′E′,点G是MN的中点,连接M′G交抛物线的对称轴于点H,过点H作直线l∥PM,点R是直线l上一点,在平面直角坐标系中是否存在一点S,使以点M′,点G,点R,点S为顶点的四边形是矩形?若存在,直接写出点S的坐标,若不存在,请说明理由.
NF取得最小值时,将△PME绕点P顺时针旋转120°后得到△PM′E′,点G是MN的中点,连接M′G交抛物线的对称轴于点H,过点H作直线l∥PM,点R是直线l上一点,在平面直角坐标系中是否存在一点S,使以点M′,点G,点R,点S为顶点的四边形是矩形?若存在,直接写出点S的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件30元,售价为每件40元,每周可卖出180件;如果每件商品的售价每上涨1元,则每周就会少卖出5件,但每件售价不能高于55元,设每件商品的售价上涨x元(x为整数),每周的销售利润为y元.
(1)求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)每件商品的售价为多少元时,每周可获得最大利润?最大利润是多少?
(3)每件商品的售价定为多少元时,每周的利润恰好是2145元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知B港口位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为16km,一艘货轮从B港口以40km/h的速度沿如图所示的BC方向航行,15min后达到C处,现测得C处位于A观测点北偏东79.8°方向,求此时货轮与A观测点之间的距离AC的长(精确到0.1km).(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,![]() ≈1.41,
≈1.41,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校对全校学生进传统文化礼仪知识测试,为了了解测试结果,随机抽取部分学生的成绩进行分析,现将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).

请你根据图中所给的信息解答下列问题:(1)本次随机抽取的人数是 人,并将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则我校被抽取的学生中有 人达标;
(3)若我校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com