
����Ŀ����У��ȫУѧ������ͳ�Ļ�����֪ʶ���ԣ�Ϊ���˽���Խ���������ȡ����ѧ���ijɼ����з������ֽ��ɼ���Ϊ�����ȼ������ϸ�һ�㡢���㣬�����Ƴ���������ͳ��ͼ������������

�������ͼ����������Ϣ����������⣺��1�����������ȡ���������� ���ˣ�������������ͳ��ͼ����������
��2������һ��������������������Ϊ���ɼ�������У����ȡ��ѧ�������� ���˴�ꣻ
��3������Уѧ����1200�ˣ�������ƴ˴β����У�ȫУ����ѧ���ж����ˣ�
���𰸡���1��120����ͼ����������2��96����3��960��.
��������
��1���������ϸ�������������ռ�İٷֱ������������ȷ���������������������Լ�һ��İٷֱȣ���ȫͳ��ͼ���ɣ�
��2�������һ��������������ռ�İٷֱȣ��������������ɵõ������
��3��������ռ�İٷֱȣ�����1200���ɵõ������
��1����������ã�24��20%=120���ˣ���
��������������Ϊ120����24+36��=60���ˣ�����һ����ռ�İٷֱ�Ϊ![]() ��100%=30%��
��100%=30%��
��ȫͳ��ͼ����ͼ��ʾ��
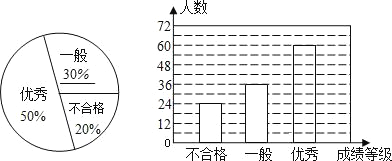
��2����������ã�36+60=96���ˣ���
���������Ϊ96�ˣ�
��3����������ã�![]() ��1200=960���ˣ���
��1200=960���ˣ���
��ȫУ����ѧ����960�ˣ�
�ʴ�Ϊ����1��120����2��96�ˣ�


 ��ְٷְټ���ϵ�д�
��ְٷְټ���ϵ�д� �����ƻ���ĩ��̶�100��ϵ�д�
�����ƻ���ĩ��̶�100��ϵ�д� �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ѧ���Ĵ�����˼ά,ѧУ���пƼ�С�����������Թ����������ĿƼ�С������Ʒ�����������˷���ͳ��,������������ͳ��ͼ��
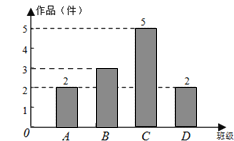
��1��ѧУ����������Ʒ���� ����;
��2��������ѡ��,��2��������2��Ů�����һ�Ƚ�����Ҫ����4λͬѧ�г�����ȥ�μӱ�����̸��,������״ͼ���б������ǡ�ó���һ��һŮ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB��90�㣬AC��BC��2������ABC��AC���е�D��ʱ����ת90��õ���A��B��C�䣬���е�B���˶�·��Ϊ![]() ����ͼ����Ӱ���ֵ����Ϊ��������
����ͼ����Ӱ���ֵ����Ϊ��������
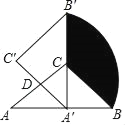
A.![]() ����
����![]() B.2C.
B.2C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
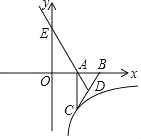
����Ŀ����ͼ��Rt��ABC�У���BAC��90����AB��2����AB��x���ϣ�BC���ϵ�����AD�ķ����ӳ��߽�y���ڵ�E��0��3��������������y��![]() ��x��0����ͼ�����C����k��ֵΪ_____��
��x��0����ͼ�����C����k��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��a��0����ͼ����x�ύ��A��B���㣬��A��B��࣬��OA��OB������y�ύ�ڵ�C.
��a��0����ͼ����x�ύ��A��B���㣬��A��B��࣬��OA��OB������y�ύ�ڵ�C.
��1����C�����꣬���ж�b�������ԣ�
��2����������κ�����ͼ��ĶԳ�����ֱ��AC���ڵ�D����֪DC��CA=1��2��ֱ��BD��y�ύ�ڵ�E������BC��
������BCE�����Ϊ8������κ����Ľ���ʽ��
������BCDΪ��������Σ���ֱ��д��OA��ȡֵ��Χ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������![]() �����ֹ���Ʒ��
�����ֹ���Ʒ��![]() ÿ��ÿ��������
ÿ��ÿ��������![]() ��105Ԫ������30Ԫ��
��105Ԫ������30Ԫ��![]() �����240Ԫ��
�����240Ԫ��![]() ������ȣ�
������ȣ�
��1������һ��![]() ��һ��
��һ��![]() �ֱ��������Ԫ��
�ֱ��������Ԫ��
��2����������65������![]() ��
��![]() �����ֹ���Ʒ��ÿ��ÿ������2��
�����ֹ���Ʒ��ÿ��ÿ������2��![]() ��1��
��1��![]() �������ڲ����ӹ��˵�����£���������
�������ڲ����ӹ��˵�����£���������![]() ����֪ÿ��ÿ�������1��
����֪ÿ��ÿ�������1��![]() ��ÿ��ÿ��ֻ������һ���ֹ���Ʒ����Ҫ��ÿ������
��ÿ��ÿ��ֻ������һ���ֹ���Ʒ����Ҫ��ÿ������![]() ��
��![]() �����ֹ���Ʒ��������ȣ���ÿ�찲��
�����ֹ���Ʒ��������ȣ���ÿ�찲��![]() ������
������![]() ��
��![]() ������
������![]() ���
���![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��3���ڣ�1����2���������£�ÿ������![]() ������5������ÿ������5��ʱ��ÿ���������䣮��ÿ����1��������ƽ��ÿ����������2Ԫ����֪
������5������ÿ������5��ʱ��ÿ���������䣮��ÿ����1��������ƽ��ÿ����������2Ԫ����֪![]() ÿ������30Ԫ����ÿ�����������ֹ���Ʒ�ɻ�õ�������
ÿ������30Ԫ����ÿ�����������ֹ���Ʒ�ɻ�õ�������![]() ��Ԫ�������ֵ����Ӧ
��Ԫ�������ֵ����Ӧ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
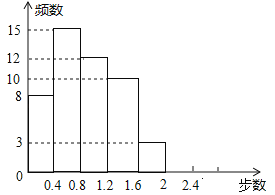
����Ŀ���ֽ����˶�����Խ��Խ����˹�ע��ϲ����ij��ȤС���������������50����ʦij�ա����˶����еIJ������������ͳ�����������������µ�ͳ��ͼ�������������������������Ϣ�������������
��1��д��a��b��ֵ����ȫƵ���ֲ�ֱ��ͼ��
��2��50����ʦ���ա����˶���ͳ�������в�������λ�����ڵ��� ���飻����Լ��40000����ʦ�����������߲�������1.2������1.2���Ľ�ʦԼ���� ������
��3������50��������Ľ�ʦ�У�ѡȡ�����߲�������16000��������16000������������ʦ���ҷ����ĵã���ѡȡ��������ʦǡ�ö���2000��������20000�����ϵĸ��ʣ�
�������� | Ƶ�� | Ƶ�� |
0��x��0.4 | 8 | a |
0.4��x��0.8 | 15 | 0.3 |
0.8��x��1.2 | 12 | 0.241 |
1.2��x��1.6 | 10 | 0.2 |
1.6��x��2 | 3 | 0.06 |
2��x��2.4 | b | 0.04 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
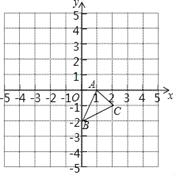
����Ŀ����ƽ��ֱ������ϵ�У���ABC��������������ֱ�ΪA��1��0����B��0����2����C��2����1����
��1����������x��ԳƵġ�AB1C1��
��2����ԭ��OΪλ�����ģ�������A2B2C2��ʹ��A2B2C2���ABC��λ�Ʊ�Ϊ2��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�����������y��![]() ��x��0��k��0ͼ���ϵ����㣨n��3n������n+1��2n����
��x��0��k��0ͼ���ϵ����㣨n��3n������n+1��2n����
��1����n��ֵ��
��2����ͼ��ֱ��lΪ����������y��x��ͼ����A�ڷ���������y��![]() ��x��0��k��0����ͼ���ϣ�����A��AB��l�ڵ�B������B��BC��x���ڵ�C������A��AD��BC�ڵ�D���ǡ�BOC�����ΪS1����ABD�����ΪS2����S1��S2��ֵ��
��x��0��k��0����ͼ���ϣ�����A��AB��l�ڵ�B������B��BC��x���ڵ�C������A��AD��BC�ڵ�D���ǡ�BOC�����ΪS1����ABD�����ΪS2����S1��S2��ֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com