[题目]某中学为了创建“最美校园图书屋新购买了一批图书.其中科普类图书平均每本的价格是文学类图书平均每本书价格的1.2倍.已知学校用12000元购买文学类图书的本数比用这些钱购买科普类图书的本数多100本.那么学校购买文学类图书平均每本书的价格是( )A.20元B.18元C.15元D.10元题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】某中学为了创建“最美校园图书屋”新购买了一批图书，其中科普类图书平均每本的价格是文学类图书平均每本书价格的1.2倍，已知学校用12000元购买文学类图书的本数比用这些钱购买科普类图书的本数多100本，那么学校购买文学类图书平均每本书的价格是（　　）

A.20元B.18元C.15元D.10元

【答案】A

【解析】

设文学类图书平均价格为x元/本，则科普类图书平均价格为1.2x元/本，根据数量=总价÷单价结合用12000元购买文学类图书的本数比用这些钱购买科普类图书的本数多100本，即可得出关于x的分式方程，解之经检验后即可得出结论．

设文学类图书平均价格为x元/本，则科普类图书平均价格为1.2x元/本，

依题意得：，

解得：x＝20，

经检验，x＝20是原方程的解，且符合题意．

故选A．

练习册系列答案

赢在起跑线快乐暑假河北少年儿童出版社系列答案

名校联盟金考卷期末大冲刺系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，CB＝CA，∠ACB＝90°，点D在边BC上(与B，C不重合)，四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：①AC＝FG；②S△FAB∶S四边形CBFG＝1∶2；③∠ABC＝∠ABF；④AD2＝FQ·AC，其中正确结论的个数是(　　)

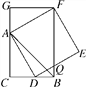
A. 1个 B. 2个 C. 3个 D. 4个

查看答案和解析>>

科目：初中数学 来源： 题型：

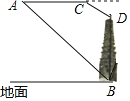
【题目】某兴趣小组同学借助无人机航拍测量某公园内一座古塔高度．如图，无人机在距离地面168米的A处，测得该塔底端点B的俯角为40°，然后向古塔方向沿水平面飞行50秒到达点C处，此时测得该塔顶端点D的俯角为60°．已知无人机的飞行速度为3米/秒，则这座古塔的高度约为_____米（参考计算：sin40°≈064．cos40°≈077．tan40°≈0.84.≈1.41. 1.73．结果精确到0.1米）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图抛物y＝﹣与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．C，D两点关于抛物线对称轴对称，连接BD交y轴于点E，抛物线对称轴交x轴于点F．

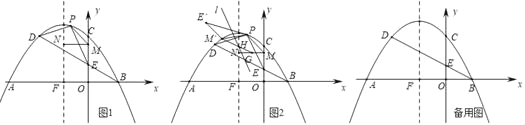
（1）点P为线段BD上方抛物线上的一点，连接PD，PE．点M是y轴上一点，过点M作MN⊥y轴交抛物线对称轴于点N．当△PDE面积最大时，求PM+MN+NF的最小值；

（2）如图2，在（1）中PM+MN+NF取得最小值时，将△PME绕点P顺时针旋转120°后得到△PM′E′，点G是MN的中点，连接M′G交抛物线的对称轴于点H，过点H作直线l∥PM，点R是直线l上一点，在平面直角坐标系中是否存在一点S，使以点M′，点G，点R，点S为顶点的四边形是矩形？若存在，直接写出点S的坐标，若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

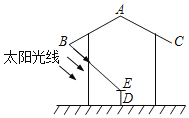
【题目】公园内一凉亭，凉亭顶部是一圆锥形的顶盖，立柱垂直于地面，在凉亭内中央位置有一圆形石桌，某数学研究性学习小组，将此凉亭作为研究对象，并绘制截面示意图，其中顶盖母线AB与AC的夹角为124°，凉亭顶盖边缘B、C到地面的距离为2.4米，石桌的高度DE为0.6米，经观测发现：当太阳光线与地面的夹角为42°时，恰好能够照到石桌的中央E处（A、E、D三点在一条直线上），请你求出圆锥形顶盖母线AB的长度．（结果精确到0.1m）（参考数据：sin62°≈0.88，tan42°≈0.90）