
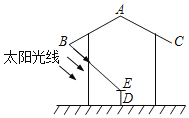
【题目】公园内一凉亭,凉亭顶部是一圆锥形的顶盖,立柱垂直于地面,在凉亭内中央位置有一圆形石桌,某数学研究性学习小组,将此凉亭作为研究对象,并绘制截面示意图,其中顶盖母线AB与AC的夹角为124°,凉亭顶盖边缘B、C到地面的距离为2.4米,石桌的高度DE为0.6米,经观测发现:当太阳光线与地面的夹角为42°时,恰好能够照到石桌的中央E处(A、E、D三点在一条直线上),请你求出圆锥形顶盖母线AB的长度.(结果精确到0.1m)(参考数据:sin62°≈0.88,tan42°≈0.90)
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】某市实施产业精准扶贫,帮助贫困户承包荒山种植某品种蜜柚.已知该蜜柚的成本价为6元/千克,到了收获季节投入市场销售时,调查市场行情后,发现该蜜柚不会亏本,且每天的销售量y(千克)与销售单价x(元)之间的函数关系如图所示.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某村农户今年共采摘蜜柚12000千克,若该品种蜜柚的保质期为50天,按照(2)的销售方式,能否在保质期内全部销售完这批蜜柚?若能,请说明理由;若不能,应定销售价为多少元时,既能销售完又能获得最大利润?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买A、B两种商品共30件,要求购买B商品的数量不高于A商品数量的2倍,且该商店购买的A、B两种商品的总费用不超过276元,那么该商店有几种购买方案?
(3)若购买A种商品m件,实际购买时A种商品下降了a(a>0)元,B种商品上涨了3a元,在(2)的条件下,此时购买这两种商品所需的最少费用为1076元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步了解八年级学生的身体素质情况,体育老师以八年级(1)班50位学生为样本进行了一分钟跳绳次数测试.根据测试结果,绘制出部分频数分布表和部分频数分布直方图.
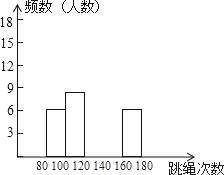
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
请结合图表完成下列问题:
(1)表中的a= ;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第 组;
(4)已知该校八年级共有学生800,请你估计一分钟跳绳次数不低于120次的八年级学生大约多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l与x轴,y轴分别交于A,B两点,且与反比例函数y=![]() (x>0)的图象交于点C,若S△AOB=S△BOC=1,则k=( )
(x>0)的图象交于点C,若S△AOB=S△BOC=1,则k=( )
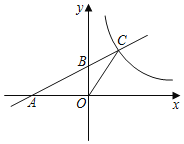
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了创建“最美校园图书屋”新购买了一批图书,其中科普类图书平均每本的价格是文学类图书平均每本书价格的1.2倍,已知学校用12000元购买文学类图书的本数比用这些钱购买科普类图书的本数多100本,那么学校购买文学类图书平均每本书的价格是( )
A.20元B.18元C.15元D.10元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=![]() x
x![]() +
+![]() x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点E.
x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点E.

(1)判断△ABC的形状,并说明理由;
(2)经过B. C两点的直线交抛物线的对称轴于点D,求D点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
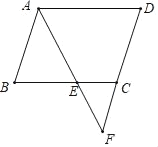
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F.
(1)若AB=4,BC=6,求EC的长;
(2)若∠EAD=50°,求∠BAE和∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011山东济南,27,9分)如图,矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线![]() 经过A、C两点,与AB边交于点D.
经过A、C两点,与AB边交于点D.
(1)求抛物线的函数表达式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式,并求出m为何值时,S取得最大值;
②当S最大时,在抛物线![]() 的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com