
����Ŀ��ij�̵깺��60��A��Ʒ��30��B��Ʒ������1080Ԫ������50��A��Ʒ��20��B��Ʒ������880Ԫ��
��1��A��B������Ʒ�ĵ��۷ֱ��Ƕ���Ԫ��
��2����֪���̵깺��A��B������Ʒ��30����Ҫ����B��Ʒ������������A��Ʒ������2�����Ҹ��̵깺���A��B������Ʒ���ܷ��ò�����276Ԫ����ô���̵��м��ֹ�����
��3��������A����Ʒm����ʵ�ʹ���ʱA����Ʒ�½���a��a��0��Ԫ��B����Ʒ������3aԪ���ڣ�2���������£���ʱ������������Ʒ��������ٷ���Ϊ1076Ԫ����m��ֵ��
���𰸡���1��A����Ʒ�ĵ���Ϊ16Ԫ��B����Ʒ�ĵ���Ϊ4Ԫ����2����4�ֹ���������������3��m��ֵ��13��
��������
��1����A����Ʒ�ĵ���ΪxԪ��B����Ʒ�ĵ���ΪyԪ�����ݵ�����ϵ���ٹ���60��A��Ʒ��Ǯ��+30��B��Ʒ��Ǯ��=1080Ԫ���ڹ���50��A��Ʒ��Ǯ��+20��B��Ʒ��Ǯ��=880Ԫ�ֱ��г����̣�������⼴�ɣ�
��2���蹺��A��Ʒ�ļ���Ϊm��������B��Ʒ�ļ���Ϊ��30-m���������ݲ��ȹ�ϵ���ٹ���B��Ʒ������������A��Ʒ������2�����ڹ����A��B������Ʒ���ܷ��ò�����276Ԫ�ɷֱ��г�����ʽ���������ɵó�m��ȡֵ��Χ���������۸��������ɣ�
��3��������Ŀ����������������������Ʒ�������ٷ���Ϊ1076Ԫ�IJ���ʽ��Ȼ���������ۣ����Ϳ�ȷ����m��ֵ��
�⣺��1����A����Ʒ�ĵ���ΪxԪ��B����Ʒ�ĵ���ΪyԪ��
![]() �����
�����![]() ��
��
��A����Ʒ�ĵ���Ϊ16Ԫ��B����Ʒ�ĵ���Ϊ4Ԫ��
��2���蹺��A����Ʒ�ļ���Ϊm��������B����Ʒ�ļ���Ϊ��30��m������
![]() ��
��
��ã�10��m��13��
��m��������
��m��10��11��12��13��
�����������ַ�����
������1����m��10��30��m��20��������A��Ʒ�ļ���Ϊ10��������B��Ʒ�ļ���Ϊ20����
������2����m��11��30��m��19��������A��Ʒ�ļ���Ϊ11��������B��Ʒ�ļ���Ϊ19����
������3����m��12��30��m��18��������A��Ʒ�ļ���Ϊ12��������B��Ʒ�ļ���Ϊ18����
������4����m��13��30��m��17��������A��Ʒ�ļ���Ϊ13��������B��Ʒ�ļ���Ϊ17����
��3��������ɵã�
m��16��a��+��30��m����4+3a����1076��
����
����4a+12��m+90a+120��1076
��10��m��13��m��������
�൱��4a+12��0ʱ����a��3����ʱ��m��10ʱȡ����Сֵ��
��4a+12����10+90a+120��1076����ã�a��16.72����ȥ����
����4a+12��0ʱ����a��3��90a+120��390��1076���ʴ�����������ڣ�
����4a+12��0ʱ����a��3����ʱ��m��13ʱ��ȡ����Сֵ��
��4a+12����13+90a+120��1076����a��21![]() ��
��
���Ͽɵã�m��ֵ��13��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ������x1��x2��x3��x4��x5��ƽ������2��������1��������3x1��2��3x2��2��3x3��2��3x4��2��3x5��2��ƽ������_____��������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
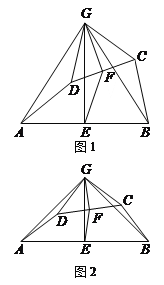
����Ŀ����ͼ1�����ı���ABCD�У���E��F�ֱ���AB��CD���е㣬����E��AB�Ĵ��ߣ�����F��CD�Ĵ��ߣ������߽��ڵ�G������AG��BG��CG��DG������AGD����BGC��
��1����֤��AD��BC��
��2����֤����AGD�ס�EGF��
��3����ͼ2����AD��BC����ֱ���ഹֱ����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y��ax2+bx+c�Ŀ������ϣ���x���ཻ��A��B���㣨��A�ڵ�B���Ҳࣩ����A������Ϊ��m��0������AB��4��
��1����գ���B������Ϊ�� �����ú�m�Ĵ���ʽ��ʾ����
��2��������AB�Ƶ�A��˳ʱ�뷽����ת135���������߽��ڵ�P����ABP�����Ϊ8��
���������ߵĽ���ʽ���ú�m�Ĵ���ʽ��ʾ����
�ڵ�0��x��1���������ϵĵ㵽x���������ֵΪ![]() ʱ����m��ֵ��
ʱ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
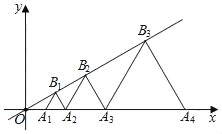
����Ŀ����ͼ��ֱ��OD��x�����е����Ϊ30�㣬OA1�ij�Ϊ1����A1A2B1����A2A3B2����A3A4B3��������AnAn+1Bn��Ϊ�ȱ������Σ���A1��A2��A3������An+1��x������������������У���B1��B2��B3������Bn��ֱ��OD���������У���ôB2019������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
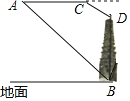
����Ŀ��ij��ȤС��ͬѧ�������˻����IJ���ij����һ�������߶ȣ���ͼ�����˻��ھ������168��A������ø����˵�B�ĸ���Ϊ40����Ȼ�������������ˮƽ�����50�뵽���C������ʱ��ø������˵�D�ĸ���Ϊ60������֪���˻��ķ����ٶ�Ϊ3��/�룬�����������ĸ߶�ԼΪ_____�ף��ο����㣺sin40���064��cos40���077��tan40���0.84.![]() ��1.41.
��1.41.![]() 1.73�������ȷ��0.1�ף�
1.73�������ȷ��0.1�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ��
�����龳
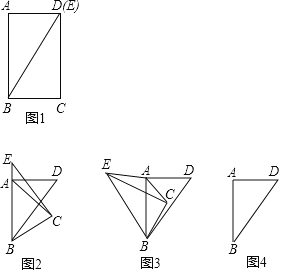
���ۺ���ʵ�����ϣ���ʦ��֯ͬѧ������������ֽƬ����ת��Ϊ���չ��ѧ�����ͼ1�����о���ֽƬABCD��AB��4cm��AD��3cm������BD��������ABCD��BD�������õ���ABD����BCE��������ABDλ�ò��䣬����BCE��ͼ1��λ�ÿ�ʼ���Ƶ�B����ʱ�뷽����ת����ת��Ϊ����0��ܦ���360������
��������
��1������BCE��ת�����У�����AE��AC��������0��ʱ��![]() ��ֵ���� ����
��ֵ���� ����
��2����ͼ2����ͼ1�е���BCE��ת������E����BA�ӳ�����ʱֹͣ��ת�������ʱ��![]() ֵ��
ֵ��
ʵ��̽��
��3����ͼ3����ͼ2�е���BCE������ת����AC��AEʱֹͣ��ת��ֱ��д����ʱ���Ķ������������AEC�������
��4����ͼ3�е���BCE������ת������ijһʱ��AC��AE���������������ܣ���˵�����ɣ�����ܣ�����ͼ4�л�����ʱ����BCE������AC��AE����ֱ��д����AEC�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
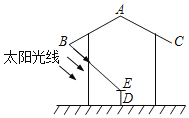
����Ŀ������һ��ͤ����ͤ������һԲ�εĶ��ǣ�������ֱ�ڵ��棬����ͤ������λ����һԲ��ʯ����ij��ѧ�о���ѧϰС�飬������ͤ��Ϊ�о��������ƽ���ʾ��ͼ�����ж���ĸ��AB��AC�ļн�Ϊ124������ͤ���DZ�ԵB��C������ľ���Ϊ2.4�ף�ʯ���ĸ߶�DEΪ0.6�ף����۲ⷢ�֣���̫�����������ļн�Ϊ42��ʱ��ǡ���ܹ��յ�ʯ��������E����A��E��D������һ��ֱ���ϣ����������Բ�ζ���ĸ��AB�ij��ȣ��������ȷ��0.1m�����ο����ݣ�sin62���0.88��tan42���0.90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���OABC�У�OA��5��OC��4��F��AB�ϵ�һ�����㣨F����A��B�غϣ�������F�ķ���������y��![]() ��k��0����ͼ����BC�߽��ڵ�E��
��k��0����ͼ����BC�߽��ڵ�E��
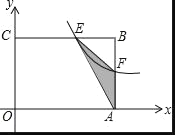
��1����FΪAB���е�ʱ����ú����ı���ʽ��
��2����kΪ��ֵʱ����EFA���������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com