
【题目】综合与实践
问题情境
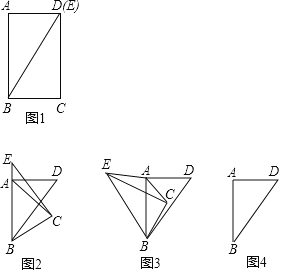
在综合与实践课上,老师组织同学们以“三角形纸片的旋转”为主题开展数学活动.如图1,现有矩形纸片ABCD,AB=4cm,AD=3cm.连接BD,将矩形ABCD沿BD剪开,得到△ABD和△BCE.保持△ABD位置不变,将△BCE从图1的位置开始,绕点B按逆时针方向旋转,旋转角为α(0°≤α<360°).
操作发现
(1)在△BCE旋转过程中,连接AE,AC,则当α=0°时,![]() 的值是 ;
的值是 ;
(2)如图2,将图1中的△BCE旋转,当点E落在BA延长线上时停止旋转,求出此时的![]() 值;
值;
实践探究
(3)如图3,将图2中的△BCE继续旋转,当AC=AE时停止旋转,直接写出此时α的度数,并求出△AEC的面积;
(4)将图3中的△BCE继续旋转,则在某一时刻AC和AE还能相等吗?如果不能,则说明理由;如果能,请在图4中画出此时的△BCE,连接AC,AE,并直接写出△AEC的面积值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)α的度数为60°,面积为(4
;(3)α的度数为60°,面积为(4![]() ﹣6)cm2;(4)(4
﹣6)cm2;(4)(4![]() +6)cm2
+6)cm2
【解析】
(1)如图1中,连接AC,理由勾股定理求出AC即可解决问题.
(2)如图2中,过点C作CF⊥AB于点F,在Rt△AFC中,求出AF,FC即可解决问题.
(3)结论:α的度数为60°.如图3中,设EC的中点为G,连接AG,过点A作AH⊥BC于点H.解直角三角形求出AG即可解决问题.
(4)结论:AC和AE还能相等,△BCE位置如图4所示:取CE的中点G,连接AG,作BH⊥AG于H.求出AG即可解决问题.
(1)如图1中,连接AC,

∵四边形ABCD是矩形,
∴∠ABC=90°,BC=AD=3,
∴AC=![]() =
=![]() =5,
=5,
∵AE=AD=3,
∴![]() =
=![]() ,
,
故答案为![]() .
.
(2)如图2中,过点C作CF⊥AB于点F,

∵四边形ABCD是矩形,AB=4,AD=3,
∴EC=4,BC=3,∠BAD=∠BCE=90°,
∴BD=BE=![]() =
=![]() =5,
=5,
∴sin∠FBC=![]() =
=![]() .cos∠FBC=
.cos∠FBC=![]() =
=![]() ,
,
在Rt△BFC中,BF=BCcos∠FBC=3×![]() =
=![]() ,FC=BCsin∠FBC=3×
,FC=BCsin∠FBC=3×![]() =
=![]() ,
,
∴AF=AB﹣BF=4﹣![]() =
=![]() ,
,
在Rt△AFC中,AC=![]() =
= =
=![]() ,
,
AE=BE﹣AB=5﹣4=1,
∴![]() .
.
(3)结论:α的度数为60°.
理由:如图3中,设EC的中点为G,连接AG,过点A作AH⊥BC于点H.

∵AC=AE,EG=GC,
∴AG⊥EC,
∵∠GCH=180°﹣∠ECB=180°﹣90°=90°,
∴∠AGC=∠GCH=∠AHC=90°,
∴四边形AGCH是矩形,
∴GC=AH=![]() EC=
EC=![]() ×4=2,
×4=2,
在Rt△ABH中,BH=![]() =
=![]() =2
=2![]() ,sin∠ABH=
,sin∠ABH=![]() ,
,
∴AG=CH=BH﹣BC=2![]() ﹣3,∠ABH=30°,
﹣3,∠ABH=30°,
∴旋转角α=90°-30°=60°,
S△AEC=![]() ECAG=
ECAG=![]() ×4×(2
×4×(2![]() ﹣3)=(4
﹣3)=(4![]() ﹣6)cm2.
﹣6)cm2.
(4)结论:AC和AE还能相等,△BCE位置如图4所示:

取CE的中点G,连接AG,作BH⊥AG于H.
同法可得:GH=BC=3,AH=2![]() ,
,
∴AG=2![]() +3,
+3,
∴S△AEC=![]() ECAG=
ECAG=![]() ×4×(2
×4×(2![]() +3)=(4
+3)=(4![]() +6)cm2.
+6)cm2.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】在元旦期间,某商场计划购进甲、乙两种商品.
(1)已知甲、乙两种商品的进价分别为30元,70元,该商场购进甲、乙两种商品共50件需要2300元,则该商场购进甲、乙两种商品各多少件?
(2)该商场共投入9500元资金购进这两种商品若干件,这两种商品的进价和售价如表所示:
甲 | 乙 | |
进价(元/件) | 30 | 70 |
售价(元/件) | 50 | 100 |
若全部销售完后可获利5000元(利润=(售价﹣进价)×销量),则该商场购进甲、乙两种商品各多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
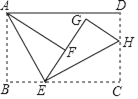
【题目】如图,矩形ABCD中,AB=4,AD=6,点E为BC上一点,将△ABE沿AE折叠得到△AEF,点H为CD上一点,将△CEH沿EH折叠得到△EHG,且F落在线段EG上,当GF=GH时,则BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买A、B两种商品共30件,要求购买B商品的数量不高于A商品数量的2倍,且该商店购买的A、B两种商品的总费用不超过276元,那么该商店有几种购买方案?
(3)若购买A种商品m件,实际购买时A种商品下降了a(a>0)元,B种商品上涨了3a元,在(2)的条件下,此时购买这两种商品所需的最少费用为1076元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截至2019年5月,山西省政府大力实施的建设“山西农谷”战略成果初现,“山西农谷”通过组建山西农谷生物科技研究院,逐步建成大学生“互联网+农业”创新创业园.某校科技小组到该创业园的全环境智能番茄特色小镇进行综合实践活动,随机调查了60株“农谷一号“番茄的挂果数量(单位:个),并绘制了如下不完靠的统计图表:
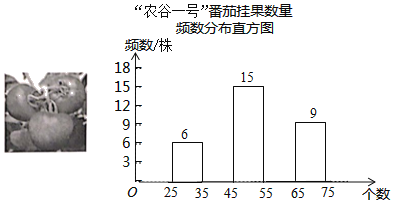
“农谷一号”番茄挂果数量统计表
挂果数量x(个) | 频数(株) | 频率 |
25≤<35 | 6 | |
35≤x<45 | 0.2 | |
45≤x<55 | 15 | a |
55≤x<65 | ||
65≤x<75 | 9 |
请结合图表中的信息解答下列问题:
(l)统计表中,a= ,若绘制“农谷一号”番茄挂果数量扇形统计图,则挂果数量在“35≤x<45”所对应扇形的圆心角度数为 ;
(2)将频数分布直方图补充完整;
(3)若所种植的“农谷一号”番茄有1000株,请估计挂果数量在“55≤x<65”范围的番茄株数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步了解八年级学生的身体素质情况,体育老师以八年级(1)班50位学生为样本进行了一分钟跳绳次数测试.根据测试结果,绘制出部分频数分布表和部分频数分布直方图.
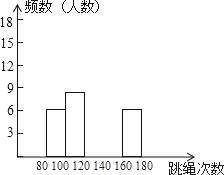
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
请结合图表完成下列问题:
(1)表中的a= ;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第 组;
(4)已知该校八年级共有学生800,请你估计一分钟跳绳次数不低于120次的八年级学生大约多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l与x轴,y轴分别交于A,B两点,且与反比例函数y=![]() (x>0)的图象交于点C,若S△AOB=S△BOC=1,则k=( )
(x>0)的图象交于点C,若S△AOB=S△BOC=1,则k=( )
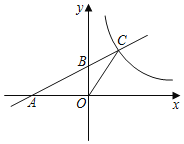
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=![]() x
x![]() +
+![]() x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点E.
x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点E.

(1)判断△ABC的形状,并说明理由;
(2)经过B. C两点的直线交抛物线的对称轴于点D,求D点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为了扩大经营,决定购进6台机器用于生产某活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示.经过预算,本次购买机器所耗资金不能超过34万元.
甲 | 乙 | |
价格(万元/台) | 7 | 5 |
每台日产量(个) | 100 | 60 |
(1)按该公司要求可以有几种购买方案?
(2)如果该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择什么样的购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com