
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c的开口向上,与x轴相交于A、B两点(点A在点B的右侧),点A的坐标为(m,0),且AB=4.
(1)填空:点B的坐标为 (用含m的代数式表示);
(2)把射线AB绕点A按顺时针方向旋转135°与抛物线交于点P,△ABP的面积为8:
①求抛物线的解析式(用含m的代数式表示);
②当0≤x≤1,抛物线上的点到x轴距离的最大值为![]() 时,求m的值.
时,求m的值.
【答案】(1)(m﹣4,0);(2)①y=![]() (x﹣m)(x﹣m+4);②m的值为:2+2
(x﹣m)(x﹣m+4);②m的值为:2+2![]() 或3﹣2
或3﹣2![]() 或2≤m≤3.
或2≤m≤3.
【解析】
(1)A的坐标为(m,0),AB=4,则点B坐标为(m-4,0);
(2)①S△ABP=![]() AByP=2yP=8,即:yP=4,求出点P的坐标为(4+m,4),即可求解;
AByP=2yP=8,即:yP=4,求出点P的坐标为(4+m,4),即可求解;
②抛物线对称轴为x=m-2.分x=m-2≥1、0≤x=m-2≤1、x=m-2≤0三种情况,讨论求解.
解:(1)A的坐标为(m,0),AB=4,则点B坐标为(m﹣4,0),故答案为(m﹣4,0);
(2)①S△ABP=![]() AByP=2yP=8,∴yP=4,
AByP=2yP=8,∴yP=4,
把射线AB绕点A按顺时针方向旋转135°与抛物线交于点P,此时,直线AP表达式中的k值为1,

设:直线AP的表达式为:y=x+b,
把点A坐标代入上式得:m+b=0,即:b=﹣m,
则直线AP的表达式为:y=x﹣m,
则点P的坐标为(4+m,4),
则抛物线的表达式为:y=a(x﹣m)(x﹣m+4),
把点P坐标代入上式得:a(4+m﹣m)(4+m﹣m+4)=4,
解得:a=![]() ,
,
则抛物线表达式为:y=![]() (x﹣m)(x﹣m+4),
(x﹣m)(x﹣m+4),
②抛物线的对称轴为:x=m﹣2,
当x=m﹣2≥1(即:m≥3)时,x=0时,抛物线上的点到x轴距离为最大值,
即:![]() (0﹣m)(0﹣m+4)=
(0﹣m)(0﹣m+4)=![]() ,解得:m=2或2±2
,解得:m=2或2±2![]() ,
,
∵m≥3,故:m=2+2![]() ;
;
当0≤x=m﹣2≤1(即:2≤m≤3)时,在顶点处,抛物线上的点到x轴距离为最大值,
即:﹣![]() (m﹣2﹣m)(m﹣2﹣m+4)=
(m﹣2﹣m)(m﹣2﹣m+4)=![]() ,符合条件,
,符合条件,
故:2≤m≤3;
当x=m﹣2≤0(即:m≤2)时,x=1时,抛物线上的点到x轴距离为最大值,
即:![]() (1﹣m)(1﹣m+4)=
(1﹣m)(1﹣m+4)=![]() ,解得:m=3或3±2
,解得:m=3或3±2![]() ,
,
∵m≤2,故:m=3﹣2![]() ;
;
综上所述,m的值为:2+2![]() 或3﹣2
或3﹣2![]() 或2≤m≤3.
或2≤m≤3.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C点,点P是抛物线上在第一象限内的一个动点,且点P的横坐标为t.
(1)求抛物线的表达式;
(2)设抛物线的对称轴为l,l与x轴的交点为D.在直线l上是否存在点M,使得四边形CDPM是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
(3)如图2,连接BC,PB,PC,设△PBC的面积为S.求S关于t的函数表达式;并求S最大时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
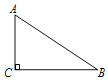
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母;(保留作图痕迹,不写作法)
①以![]() 为边在
为边在![]() 上方外作等边三角形
上方外作等边三角形![]() ;
;
②作![]() 的中线
的中线![]() ;
;
(2)计算:![]() 的长为_______.
的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店计划购进一批甲、乙两种款式的运动服进行销售,进价和售价如下表所示:
运动服款式 | 甲 | 乙 |
进价(元/套) | 80 | 100 |
售价(元/套) | 120 | 160 |
若购进两种款式的运动服共300套,且投入资金不超过26800元.
(1) 该服装店应购进甲款运动服至少多少套?
(2)若服装店购进甲款运动服的进价每套降低a元,并保持这两款运动服的售价不变,且最多购进240套甲款运动服.如果这批运动服售出后,服装店刚好获利18480元,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
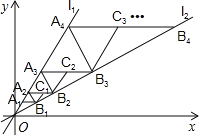
【题目】如图,点A1在直线l1:y=![]() x上,过点A1作x轴的平行线交直线l2:y=
x上,过点A1作x轴的平行线交直线l2:y=![]() x于点B1,
x于点B1,
过点B1作l2的垂线交l1于点A2,过点A2作x轴的平行线交直线l2于点B2,过点B2作l2的垂线交l1于点A3,过点A3作x轴的平行线交直线l2于点B3,……,过点B1,B2,B3,……,分别作l1的平行线交A2B2于点C1,交A3B3于点C2,交A4B4于点C3,……,按此规律继续下去,若OA1=1,则点![]() 的坐标为_______________.
的坐标为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线![]() (a≠0)与x轴的交点为A、B(A在B的左边)且AB=3,与y轴交于C
(a≠0)与x轴的交点为A、B(A在B的左边)且AB=3,与y轴交于C
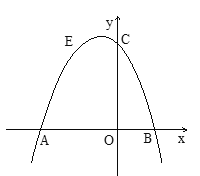
(1)求A、B两点的坐标.
(2)若抛物线过点E(-1,2),求抛物线的解析式.
(3)在x轴的下方的抛物线上是否存在一点P使得△PAC的面积为3,若存在求出P点的坐标,不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
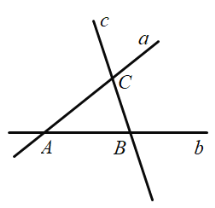
【题目】某地为了促进旅游业的发展,要在如图所示的三条公路![]() ,
,![]() ,
,![]() 围成的一块地上修建一个度假村,要使这个度假村到
围成的一块地上修建一个度假村,要使这个度假村到![]() ,
,![]() 两条公路的距离相等,且到
两条公路的距离相等,且到![]() ,
,![]() 两地的距离相等,下列选址方法绘图描述正确的是( )
两地的距离相等,下列选址方法绘图描述正确的是( )
A.画![]() 的平分线,再画线段
的平分线,再画线段![]() 的垂直平分线,两线的交点符合选址条件
的垂直平分线,两线的交点符合选址条件
B.先画![]() 和
和![]() 的平分线,再画线段
的平分线,再画线段![]() 的垂直平分线,三线的交点符合选址条件
的垂直平分线,三线的交点符合选址条件
C.画三个角![]() ,
,![]() 和
和![]() 三个角的平分线,交点即为所求
三个角的平分线,交点即为所求
D.画![]() ,
,![]() ,
,![]() 三条线段的垂直平分线,交点即为所求
三条线段的垂直平分线,交点即为所求
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com