
【题目】如图,点A1在直线l1:y=![]() x上,过点A1作x轴的平行线交直线l2:y=
x上,过点A1作x轴的平行线交直线l2:y=![]() x于点B1,
x于点B1,
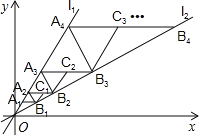
过点B1作l2的垂线交l1于点A2,过点A2作x轴的平行线交直线l2于点B2,过点B2作l2的垂线交l1于点A3,过点A3作x轴的平行线交直线l2于点B3,……,过点B1,B2,B3,……,分别作l1的平行线交A2B2于点C1,交A3B3于点C2,交A4B4于点C3,……,按此规律继续下去,若OA1=1,则点![]() 的坐标为_______________.
的坐标为_______________.
【答案】![]()
【解析】
根据两直线的解析式分别求![]() 与
与![]() 的坐标坐标,求出
的坐标坐标,求出![]() 等线段的长,然后根据四边形
等线段的长,然后根据四边形![]() 是菱形求解进而代入
是菱形求解进而代入![]() 计算即可.
计算即可.
解:∵![]() ,
,
∴l1与x轴的夹角为60°,
∵![]() ,
,
∴l2与x轴的夹角为30°,
∵点B1作l2的垂线交l1于点A2,
∴![]() 是等边三角形,
是等边三角形,
同理可得![]() 等边三角形
等边三角形
∴四边形![]() 是菱形;
是菱形;
∵OA1=1,
∴点A1的坐标为:![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴点B1的横坐标为![]() ,
,
∴点A2的横坐标为: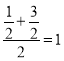 ,
,
∴OA2=2,
∴![]() ,
,
∴![]() ,
,
∴点A2的纵坐标为![]() ,
,
∴点C1的横坐标为:2,
即点C1的坐标为(21,![]() );
);
∴点A3的横坐标为2,
∴点C2的横坐标为:2+2=4,
∵点A3的纵坐标为2![]()
∴点C2的横坐标为:2![]() ,
,
故点C2的坐标为(22,21![]() ),
),
…
则点Cn的坐标为(2n,![]() ).
).
当![]() 时,则有
时,则有![]() 为
为![]()
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中,有四个完全相同的小球,把它们分别标号为1,﹣2,3,4,随机摸取一个小球记下标号后放回,再随机摸取一个小球记下标号,则两次摸取的小球的标号之积为负数的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
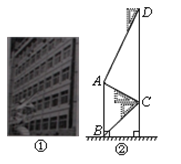
【题目】腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图11①).为了测量雕塑的高度,小明在二楼找到一点C,利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图10②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c的开口向上,与x轴相交于A、B两点(点A在点B的右侧),点A的坐标为(m,0),且AB=4.
(1)填空:点B的坐标为 (用含m的代数式表示);
(2)把射线AB绕点A按顺时针方向旋转135°与抛物线交于点P,△ABP的面积为8:
①求抛物线的解析式(用含m的代数式表示);
②当0≤x≤1,抛物线上的点到x轴距离的最大值为![]() 时,求m的值.
时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=3,BC=1,点D是斜边上一点,且AD=4BD.
(1)求tan∠BCD的值;
(2)过点B的⊙O与边AC相切,切点为AC的中点E,⊙O与直线BC的另一个交点为F.
(ⅰ)求⊙O的半径;
(ⅱ) 连接AF,试探究AF与CD的位置关系,并说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小米先从盒子中随机取出一个小球,记下数字为x,且不放回盒子,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小米、小华各取一次小球所确定的点(x,y)落在反比例函数y=![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加一个知识竞赛,该竞赛试题由10道选择题构成,每小题有四个选项,且只有一个选项正确.其给分标准为:答对一题得2分,答错一题扣1分,不答得0分,若10道题全部答对则额外奖励5分.小明对其中的8道题有绝对把握答对,剩下2道题完全不知道该选哪个选项.
(1)对于剩下的2道题,若小明都采用随机选择一个选项的做法,求两小题都答错的概率;
(2)从预期得分的角度分析,采用哪种做法解答剩下2道题更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() (k≠0)的图像与一次函数y=-x+b的图像在第一象限交于A、B两点,BC⊥x轴于点C,若△OBC的面积为2,且A点的纵坐标为4,B点的纵坐标为1.
(k≠0)的图像与一次函数y=-x+b的图像在第一象限交于A、B两点,BC⊥x轴于点C,若△OBC的面积为2,且A点的纵坐标为4,B点的纵坐标为1.
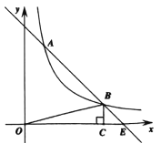
(1)求反比例函数、一次函数的表达式及直线AB与x轴交点E的坐标;
(2)已知点D(t,0)(t>0),过点D作垂直于x轴的直线,在第一象限内与一次函数y=-x+b的图像相交于点P,与反比函数![]() 上的图像相交于点Q,若点P位于点Q的上方,请结合函数图像直接写出此时t的取值范围.
上的图像相交于点Q,若点P位于点Q的上方,请结合函数图像直接写出此时t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com