
【题目】如图抛物线![]() (a≠0)与x轴的交点为A、B(A在B的左边)且AB=3,与y轴交于C
(a≠0)与x轴的交点为A、B(A在B的左边)且AB=3,与y轴交于C
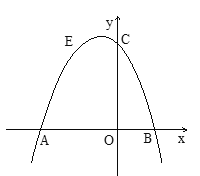
(1)求A、B两点的坐标.
(2)若抛物线过点E(-1,2),求抛物线的解析式.
(3)在x轴的下方的抛物线上是否存在一点P使得△PAC的面积为3,若存在求出P点的坐标,不存在说明理由.
【答案】(1)A(-2,0)B(1,0);(2)![]() ;(3)存在点P(-3,-4)使△PAC面积为3
;(3)存在点P(-3,-4)使△PAC面积为3
【解析】
(1)由解析式得抛物线对称轴为,又因为A在B的左边且AB=3,即可求出A、B的坐标;
(2)由(1)中的B点坐标结合E点的坐标,即可求得抛物线的解析式;
(3)由题意知,△ABC的面积为3,过B作BM∥AC,交y轴于M,交抛物线于点P,则△PAC面积为3,之后根据相似求得M坐标,再求得BM解析式,联立方程组即可求得答案.
解:(1)由解析式得抛物线对称轴为![]() ,交x轴于D,
,交x轴于D,
又∵AB=3,
∴AD=BD=![]() ,
,
∴AO=2,BO=1,
∴A(-2,0)B(1,0)
(2)把B(1,0)E(-1,2)代入解析式得![]() ,
,
解得![]() ,
,
故抛物线的解析式为![]() ;
;
(3)由(2)中抛物线可知C(0,2),
∴![]() ,
,
过B作BMAC,交y轴于M,交抛物线于点P,

则△PAC面积为3(同底等高),
由△AOC∽△BOM可得OM=1即M(0,-1),
易得直线BM解析式为y=x-1,
联立构成方程组得![]()
解得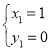 ,
,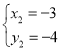
∵点P在x轴下方,
∴存在点P(-3,-4)使△PAC面积为3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c的开口向上,与x轴相交于A、B两点(点A在点B的右侧),点A的坐标为(m,0),且AB=4.
(1)填空:点B的坐标为 (用含m的代数式表示);
(2)把射线AB绕点A按顺时针方向旋转135°与抛物线交于点P,△ABP的面积为8:
①求抛物线的解析式(用含m的代数式表示);
②当0≤x≤1,抛物线上的点到x轴距离的最大值为![]() 时,求m的值.
时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小米先从盒子中随机取出一个小球,记下数字为x,且不放回盒子,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小米、小华各取一次小球所确定的点(x,y)落在反比例函数y=![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象与正比例函数
的图象与正比例函数![]() 图象交于点
图象交于点![]() ,且点
,且点![]() 的横坐标为2.
的横坐标为2.
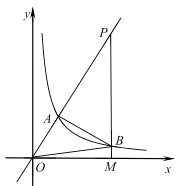
(1)求反比例函数的表达式;
(2)若射线![]() 上有一点
上有一点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 与
与![]() 轴垂直,垂足为
轴垂直,垂足为![]() ,交反比例函数图象于点
,交反比例函数图象于点![]() ,连接
,连接![]() ,
,![]() ,请求出
,请求出![]() 的面积.
的面积.
(3)定义:横纵坐标均为整数的点称为“整点”.在(2)的条件下,请探究边![]() ,
,![]() 与反比例函数图象围成的区域内(不包括边界)“整点”的个数.
与反比例函数图象围成的区域内(不包括边界)“整点”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加一个知识竞赛,该竞赛试题由10道选择题构成,每小题有四个选项,且只有一个选项正确.其给分标准为:答对一题得2分,答错一题扣1分,不答得0分,若10道题全部答对则额外奖励5分.小明对其中的8道题有绝对把握答对,剩下2道题完全不知道该选哪个选项.
(1)对于剩下的2道题,若小明都采用随机选择一个选项的做法,求两小题都答错的概率;
(2)从预期得分的角度分析,采用哪种做法解答剩下2道题更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组为测量一颗古树BH和教学楼CG的高,测角仪高AF=2米,先在A处测得古树顶端H的仰角∠HFE为45°,此时教学楼顶端G恰好在视线FH上,再向前走20米到达B处(AB=20米),又测得教学楼顶端G的仰角∠GED为60°.点A、B、C三点在同一水平线上.

(1)求古树BH的高;
(2)求教学楼CG的高.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
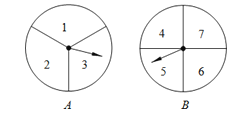
【题目】甲、乙两人用如图的两个分格均匀的转盘A、B做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:
(1)用列表格或画树状图的方法表示游戏所有可能出现的结果.
(2)求甲、乙两人获胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com