
����Ŀ����ͼ1����֪������y����x2+bx+c��x�ύ��A����1��0����B��3��0�����㣬��y�ύ��C�㣬��P�����������ڵ�һ�����ڵ�һ�����㣬�ҵ�P�ĺ�����Ϊt��
��1���������ߵı���ʽ��
��2���������ߵĶԳ���Ϊl��l��x��Ľ���ΪD����ֱ��l���Ƿ���ڵ�M��ʹ���ı���CDPM��ƽ���ı��Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
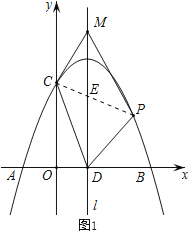
��3����ͼ2������BC��PB��PC�����PBC�����ΪS����S����t�ĺ�������ʽ������S���ʱ��P�����꣮

���𰸡���1��y����x2+2x+3����2����ֱ��l�ϴ��ڵ�M��ʹ���ı���CDPM��ƽ���ı��Σ���M������Ϊ��1��6������3��S����![]() t2+
t2+![]() t����t ��
t����t ��![]() ʱ��S�����ֵ����ʱP��
ʱ��S�����ֵ����ʱP��![]() ��
��![]() ��
��
��������
��1���ѵ�A��B�������y����x2+bx+c�����ô���ϵ������⼴�ɣ�
��2�������C��D���꣬����ֱ��l�ϴ��ڵ�M��ʹ���ı���CDPM��ƽ���ı��Σ�����ƽ���ı������ʣ������P���꣬���������M���ꣻ
��3������P��PF��y�ᣬ��BC�ڵ�F�����ֱ��BC����ʽ����ʾ���߶�PF��������![]() ���ɵõ�S����t�ĺ�������ʽ���ٸ��ݶ��κ��������ʼ�����⣮
���ɵõ�S����t�ĺ�������ʽ���ٸ��ݶ��κ��������ʼ�����⣮
�⣺��1����A����1��0����B��3��0������y����x2+bx+c��
![]() ����ã�
����ã�![]() ��
��
�������ߵı���ʽΪy����x2+2x+3��
��2����ͼ1�У�����PC���������߶Գ���l�ڵ�E��
��������y����x2+bx+c��x�ύ��A����1��0����B��3��0�����㣬
�������ߵĶԳ���Ϊֱ��x��1��
��x��0ʱ��y����x2+2x+3��3��
���C��������0��3����
���ı���CDPM��ƽ���ı��Σ���CE��PE��DE��ME��
�ߵ�C�ĺ�����Ϊ0����E�ĺ�����Ϊ1��
���P�����t��1��2��0��2��
���P��������2��3����
���E��������1��3����
���M��������1��6����
����ֱ��l�ϴ��ڵ�M��ʹ���ı���CDPM��ƽ���ı��Σ���M������Ϊ��1��6����
��3����ͼ2�У�����P��PF��y�ᣬ��BC�ڵ�F��
��ֱ��BC�Ľ���ʽΪy��mx+n��m��0����
��B��3��0����C��0��3������y��mx+n��
![]() ����ã�
����ã�![]() ��
��
��ֱ��BC�Ľ���ʽΪy����x+3��
�ߵ�P������Ϊ��t����t2+2t+3����
���F��������t����t+3����
��PF����t2+2t+3������t+3������t2+3t��
��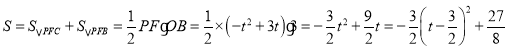 ��
��
�൱t ��![]() ʱ��S�����ֵ����ʱP��
ʱ��S�����ֵ����ʱP��![]() ��
��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() �����ߣ���
�����ߣ���![]() ����
����![]() �Ƶ�
�Ƶ�![]() ��ת
��ת![]() �õ�
�õ�![]() ����
����![]() _______
_______![]() ��
��![]() �����_________
�����_________![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ŀڴ��У����ĸ���ȫ��ͬ��С�����Ƿֱ���Ϊ1����2��3��4�������ȡһ��С����±�ź�Żأ��������ȡһ��С����±�ţ���������ȡ��С��ı��֮��Ϊ�����ĸ���Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ���뷴��������y=![]() ��ͼ���ڵ�A����3��m+8����B��n����6�����㣮
��ͼ���ڵ�A����3��m+8����B��n����6�����㣮
��1����һ�κ����뷴���������Ľ���ʽ��
��2������AOB�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֻҪ���˶��׳�һ�㰮�����罫������õ��˼䡱�������ͷ��������ڼ䣬ȫ����������һ�ģ���־�ɳǣ�����ʱ�裮ij������������Ԯ��������飬��2500������ӻԾ�����װ��ģ���������Ա�������˲��־����������ͳ��ͼ��ͼ��

��1�����㱾�ι���������������������ͼ����������
��2������ͳ�����������Ƹ��������20Ԫ���ϣ���20Ԫ���ľ����ж����ˣ�
��3����������1���й���Ա��3��Ů����Ա����Ҫ���������ѡ2������Ա���롰�������ء�������������б�������״ͼ�����ǡ��ѡ����1��1Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��ڡ���һ��������й涨���˿�ÿ����100Ԫ���ܻ��һ���н�����.Ϊ�˻�Ծ����.����������齱������
����һ��ת��ת��![]() һ�Σ�ת����ɫ����ȡһ�ݽ�Ʒ��
һ�Σ�ת����ɫ����ȡһ�ݽ�Ʒ��
��������ת��ת��![]() ���Σ����ζ�ת����ɫ����ȡһ�ݽ�Ʒ.������ת�̶���ƽ���ֳ�3�ݣ�
���Σ����ζ�ת����ɫ����ȡһ�ݽ�Ʒ.������ת�̶���ƽ���ֳ�3�ݣ�
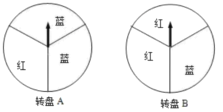
��1����ת��һ��![]() ת�̣�����ȡһ�ݽ�Ʒ�ĸ��ʣ�
ת�̣�����ȡһ�ݽ�Ʒ�ĸ��ʣ�
��2���������һ�γ齱���ᣬ���ѡ���ĸ�������������б�������״ͼ˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
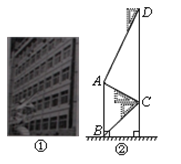
����Ŀ���ڷ���ѧ�ڽ�ѧ¥ǰ�½���һ�����ڷ������ܣ���ͼ11�٣���Ϊ�˲������ܵĸ߶ȣ�С���ڶ�¥�ҵ�һ��C���������ǰ��õ��ܶ���A�������Ϊ30�����ײ�B��ĸ���Ϊ45����С������¥�ҵ�һ��D���������ǰ���A��ĸ���Ϊ60������ͼ10�ڣ�������֪CDΪ10�ף����������AB�ĸ߶ȣ��������ȷ��0��1�ף��ο�����![]() =1��73��
=1��73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y��ax2+bx+c�Ŀ������ϣ���x���ཻ��A��B���㣨��A�ڵ�B���Ҳࣩ����A������Ϊ��m��0������AB��4��
��1����գ���B������Ϊ�� �����ú�m�Ĵ���ʽ��ʾ����
��2��������AB�Ƶ�A��˳ʱ�뷽����ת135���������߽��ڵ�P����ABP�����Ϊ8��
���������ߵĽ���ʽ���ú�m�Ĵ���ʽ��ʾ����
�ڵ�0��x��1���������ϵĵ㵽x���������ֵΪ![]() ʱ����m��ֵ��
ʱ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���μ�һ��֪ʶ�������þ���������10��ѡ����ɣ�ÿС�����ĸ�ѡ���ֻ��һ��ѡ����ȷ������ֱ�Ϊ�����һ���2�֣����һ���1�֣������0�֣���10����ȫ���������⽱��5�֣�С�������е�8�����о����մ�ԣ�ʣ��2������ȫ��֪����ѡ�ĸ�ѡ�
��1������ʣ�µ�2���⣬��С�����������ѡ��һ��ѡ�������������С�ⶼ����ĸ��ʣ�
��2����Ԥ�ڵ÷ֵĽǶȷ��������������������ʣ��2��������㣿
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com