
【题目】如图,四边形![]() 内接于
内接于![]() ,
,![]() 是
是![]() 的直径,
的直径,![]() ,垂足为点
,垂足为点![]() 平分
平分![]() .
.
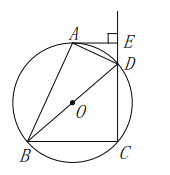
(1)![]() 是
是![]() 的切线吗?请说明理由;
的切线吗?请说明理由;
(2)若![]() 求
求![]() 的长.
的长.
 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
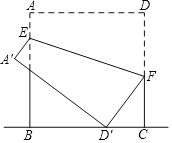
【题目】如图,正方形ABCD的边长是9,点E是AB边上的一个动点,点F是CD边上一点,CF=4,连接EF,把正方形ABCD沿EF折叠,使点A,D分别落在点A′,D′处,当点D′落在直线BC上时,线段AE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
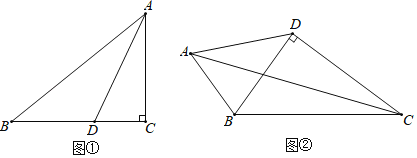
【题目】如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B= °;
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
(3)如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中,有四个完全相同的小球,把它们分别标号为1,﹣2,3,4,随机摸取一个小球记下标号后放回,再随机摸取一个小球记下标号,则两次摸取的小球的标号之积为负数的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c的开口向上,与x轴相交于A、B两点(点A在点B的右侧),点A的坐标为(m,0),且AB=4.
(1)填空:点B的坐标为 (用含m的代数式表示);
(2)把射线AB绕点A按顺时针方向旋转135°与抛物线交于点P,△ABP的面积为8:
①求抛物线的解析式(用含m的代数式表示);
②当0≤x≤1,抛物线上的点到x轴距离的最大值为![]() 时,求m的值.
时,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com