
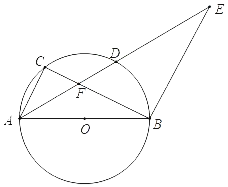
【题目】如图,AB是⊙O的直径,点C是圆上一点,点D是![]() 的中点,延长AD至点E,使得AB=BE.
的中点,延长AD至点E,使得AB=BE.
(1)求证:△ACF∽△EBF;
(2)若BE=10,tanE=![]() ,求CF的长.
,求CF的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)由圆周角定理及等腰三角形的性质可得出∠CAF=∠E,结合对顶角相等(∠AFC=∠EFB)可证出△ACF∽△EBF;
(2)由AB为直径可得出∠ACB=90°,利用相似三角形的性质可得出∠EBF=90°,由BE=10,tanE=![]() 结合相似三角形的性质可得出BF=
结合相似三角形的性质可得出BF=![]() ,AC=3CF,在Rt△ABC中利用勾股定理可得出关于CF长度的一元二次方程,解之取其正值即可得出结论.
,AC=3CF,在Rt△ABC中利用勾股定理可得出关于CF长度的一元二次方程,解之取其正值即可得出结论.
(1)证明:∵点D是![]() 的中点,
的中点,
∴∠CAD=∠BAE.
∵AB=BE,
∴∠BAE=∠E,
∴∠CAF=∠E.
又∵∠AFC=∠EFB,
∴△ACF∽△EBF;
(2)解:∵AB为⊙O的直径,
∴∠ACB=90°.
∵△ACF∽△EBF,
∴∠EBF=∠ACF=90°.
∵BE=10,tanE=![]() ,
,
∴BF=BEtanE=![]() .
.
∵∠CAF=∠E,
∴AC=3CF.
在Rt△ABC中,∠ACB=90°,AB=BE=10,AC=3CF,BC=CF+![]() ,
,
∴AB2=AC2+BC2,即102=9CF2+(CF+![]() )2,
)2,
解得:CF=![]() 或CF=﹣
或CF=﹣![]() (舍去).
(舍去).
∴CF的长为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图①,定义:直线![]() 与x、y轴分别相交于A、B两点,将
与x、y轴分别相交于A、B两点,将![]() 绕着点O逆时针旋转90°得到
绕着点O逆时针旋转90°得到![]() ,过点A、B、D的抛物线P叫做直线
,过点A、B、D的抛物线P叫做直线![]() 的“纠缠抛物线”,反之,直线
的“纠缠抛物线”,反之,直线![]() 叫做P的“纠缠直线",两线“互为纠缠线”.
叫做P的“纠缠直线",两线“互为纠缠线”.
(1)若![]() ,则纠缠物线P的函数解析式是____________.
,则纠缠物线P的函数解析式是____________.
(2)判断并说明![]() 与
与![]() 是否“互为纠缠线”.
是否“互为纠缠线”.
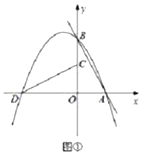
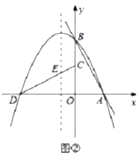
(3)如图②,若纠缠直线![]() ,纠缠抛物线P的对称轴与
,纠缠抛物线P的对称轴与![]() 相交于点E,点F在
相交于点E,点F在![]() 上,点Q在P的对称轴上,当以点C、E、Q、F为顶点的四边形是以
上,点Q在P的对称轴上,当以点C、E、Q、F为顶点的四边形是以![]() 为一边的平行四边形时,求点Q的坐标.
为一边的平行四边形时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成m种不同的等腰三角形,为探究m与n之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
(1)用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?此时,显然能搭成一种等腰三角形.所以,当n=3时,m=1
(2)用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形,所以,当n=4时,m=0
(3)用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形?若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形,所以,当n=5时,m=1
(4)用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形?若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形,所以,当n=6时,m=1
综上所述,可得表①
n | 3 | 4 | 5 | 6 |
m | 1 | 0 | 1 | 1 |
探究二:
(1)用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?(仿照上述探究方法,写出解答过程,并把结果填在表②中)
(2)分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?(只需把结果填在表②中)
n | 7 | 8 | 9 | 10 |
m |
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,…
解决问题:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设n分别等于4k﹣1、4k、4k+1、4k+2,其中k是整数,把结果填在表 ③中)
n | 4k﹣1 | 4k | 4k+1 | 4k+2 |
m |
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)其中面积最大的等腰三角形每个腰用了 根木棒.(只填结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】使得函数值为0的自变量的值称为函数的零点.例如,对于函数y=x﹣1,令y=0可得x=1,我们说1是函数y=x﹣1的零点.已知函数y=x2﹣2mx﹣2(m+3)(m为常数)
(1)当m=0时,求该函数的零点.
(2)证明:无论m取何值,该函数总有两个零点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1=k1x+b与反比例函数![]() 的图象交于A,B两点(点A在点B左侧),已知点A的坐标是(6,2)点B的纵坐标是﹣3.
的图象交于A,B两点(点A在点B左侧),已知点A的坐标是(6,2)点B的纵坐标是﹣3.
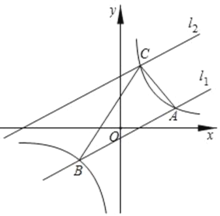
(1)求反比例函数和直线l1的表达式;
(2)根据图象直接写出k1x+b>![]() 的解集;
的解集;
(3)将直线l1:![]() 沿y轴向上平移后的直线l2与反比例函数
沿y轴向上平移后的直线l2与反比例函数![]() 在第一象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第一象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格相同),购买1个足球和2个篮球共需270元;购买2个足球和3个篮球共需464元.
(1)问足球和篮球的单价各是多少元?
(2)若购买足球和篮球共20个,且购买篮球的个数不超过足球个数的2倍,购买球的总费用不超过1910元,问该学校有哪几种不同的购买方案?哪种方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
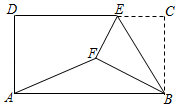
【题目】如图,在矩形ABCD中,AB=4,BC=![]() ,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=
,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=![]() ,则CE=_____.
,则CE=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com