
【题目】为迎接“世界华人炎帝故里寻根节”,某工厂接到一批纪念品生产订单,按要求在15天内完成,约定这批纪念品的出厂价为每件20元,设第x天(1≤x≤15,且x为整数)每件产品的成本是p元,p与x之间符合一次函数关系,部分数据如表:
天数(x) | 1 | 3 | 6 | 10 |
每件成本p(元) | 7.5 | 8.5 | 10 | 12 |
任务完成后,统计发现工人李师傅第x天生产的产品件数y(件)与x(天)满足如下关系:y=![]() ,
,
设李师傅第x天创造的产品利润为W元.
(1)直接写出p与x,W与x之间的函数关系式,并注明自变量x的取值范围:
(2)求李师傅第几天创造的利润最大?最大利润是多少元?
(3)任务完成后.统计发现平均每个工人每天创造的利润为299元.工厂制定如下奖励制度:如果一个工人某天创造的利润超过该平均值,则该工人当天可获得20元奖金.请计算李师傅共可获得多少元奖金?
【答案】(1)W=![]() ;(2)李师傅第8天创造的利润最大,最大利润是324元;(3)李师傅共可获得160元奖金.
;(2)李师傅第8天创造的利润最大,最大利润是324元;(3)李师傅共可获得160元奖金.
【解析】(1)根据题意和表格中的数据可以求得p与x,W与x之间的函数关系式,并注明自变量x的取值范围:
(2)根据题意和题目中的函数表达式可以解答本题;
(3)根据(2)中的结果和不等式的性质可以解答本题.
(1)设p与x之间的函数关系式为p=kx+b,则有
![]() ,解得,
,解得,![]() ,
,
即p与x的函数关系式为p=0.5x+7(1≤x≤15,x为整数),
当1≤x<10时,
W=[20﹣(0.5x+7)](2x+20)=﹣x2+16x+260,
当10≤x≤15时,
W=[20﹣(0.5x+7)]×40=﹣20x+520,
即W=![]() ;
;
(2)当1≤x<10时,
W=﹣x2+16x+260=﹣(x﹣8)2+324,
∴当x=8时,W取得最大值,此时W=324,
当10≤x≤15时,
W=﹣20x+520,
∴当x=10时,W取得最大值,此时W=320,
∵324>320,
∴李师傅第8天创造的利润最大,最大利润是324元;
(3)当1≤x<10时,
令﹣x2+16x+260=299,得x1=3,x2=13,
当W>299时,3<x<13,
∵1≤x<10,
∴3<x<10,
当10≤x≤15时,
令W=﹣20x+520>299,得x<11.05,
∴10≤x≤11,
由上可得,李师傅获得奖金的月份是4月到11月,李师傅共获得奖金为:20×(11﹣3)=160(元),
即李师傅共可获得160元奖金.


科目:初中数学 来源: 题型:
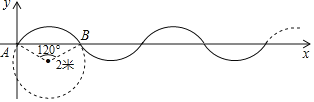
【题目】如图,在单位长度为1米的平面直角坐标系中,曲线是由半径为2米,圆心角为![]() 的
的![]() 多次复制并首尾连接而成.现有一点P从A(A为坐标原点)出发,以每秒
多次复制并首尾连接而成.现有一点P从A(A为坐标原点)出发,以每秒![]() 米的速度沿曲线向右运动,则在第2019秒时点P的纵坐标为( )
米的速度沿曲线向右运动,则在第2019秒时点P的纵坐标为( )
A. ﹣2B. ﹣1C. 0D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
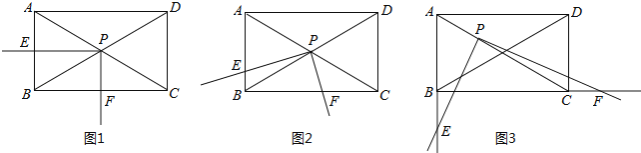
(1)当PE⊥AB,PF⊥BC时,如图1,则![]() 的值为 ;
的值为 ;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求![]() 的值;
的值;
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3,![]() 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+4的图象与反比例![]() (k为常数,且k≠0)的图象交于A(1,a),B(b,1)两点,
(k为常数,且k≠0)的图象交于A(1,a),B(b,1)两点,

(1)求反比例函数的表达式及点A,B的坐标
(2)在x轴上找一点,使PA+PB的值最小,求满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
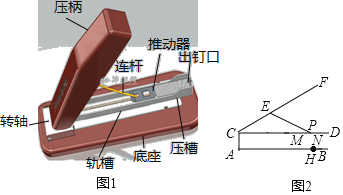
【题目】如图1是某品牌订书机,其截面示意图如图2所示.订书钉放置在轨槽CD内的MD处,由连接弹簧的推动器MN推紧,连杆EP一端固定在压柄CF上的点E处,另一端P在DM上移动.当点P与点M重合后,拉动压柄CF会带动推动器MN向点C移动.使用时,压柄CF的端点F与出钉口D重合,纸张放置在底座AB的合适位置下压完成装订(即点D与点H重合).已知CA⊥AB,CA=2cm,AH=12cm,CE=5cm,EP=6cm,MN=2cm.
(1)求轨槽CD的长(结果精确到0.1);
(2)装入订书钉需打开压柄FC,拉动推动器MN向点C移动,当∠FCD=53°时,能否在ND处装入一段长为2.5cm的订书钉?(参考数据:![]() ≈2.24,
≈2.24,![]() ≈6.08,sin53°≈0.80,cos53°≈0.60)
≈6.08,sin53°≈0.80,cos53°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:
①abc>0;
②b2﹣4ac>0;
③9a﹣3b+c=0;
④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;
⑤5a﹣2b+c<0.
其中正确的个数有( )
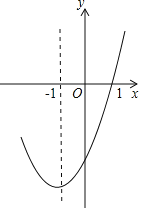
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 和点
和点![]() 是反比例函数
是反比例函数![]() 图象上的两点,一次函数
图象上的两点,一次函数![]() 的图象经过点
的图象经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() .已知
.已知![]() 与
与![]() 的面积满足
的面积满足![]() .
.

(1)![]() = _____,
= _____,![]() = _____;
= _____;
(2)已知点![]() 在线段
在线段![]() 上,当
上,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了满足师生的阅读需求,某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册.
(1)求这两年藏书的年均增长率;
(2)经统计知:中外古典名著的册数在2016年底仅占当时藏书总量的5.6%,在这两年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书的年均增长率,那么到2018年底中外古典名著的册数占藏书总量的百分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线交于点O,DF∥AC,CF∥BD.

(1)求证:四边形OCFD是矩形;(2)若AD=5,BD=8,计算tan∠DCF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com