
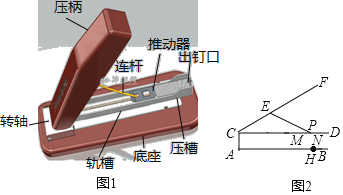
【题目】如图1是某品牌订书机,其截面示意图如图2所示.订书钉放置在轨槽CD内的MD处,由连接弹簧的推动器MN推紧,连杆EP一端固定在压柄CF上的点E处,另一端P在DM上移动.当点P与点M重合后,拉动压柄CF会带动推动器MN向点C移动.使用时,压柄CF的端点F与出钉口D重合,纸张放置在底座AB的合适位置下压完成装订(即点D与点H重合).已知CA⊥AB,CA=2cm,AH=12cm,CE=5cm,EP=6cm,MN=2cm.
(1)求轨槽CD的长(结果精确到0.1);
(2)装入订书钉需打开压柄FC,拉动推动器MN向点C移动,当∠FCD=53°时,能否在ND处装入一段长为2.5cm的订书钉?(参考数据:![]() ≈2.24,
≈2.24,![]() ≈6.08,sin53°≈0.80,cos53°≈0.60)
≈6.08,sin53°≈0.80,cos53°≈0.60)
【答案】(1)12.6(cm).(2)能在ND处装入一段长为2.5cm的订书钉.
【解析】
(1)由题意CD=CH,利用勾股定理求出CH即可.
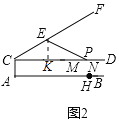
(2)如图2中,作EK⊥PC于K.解直角三角形求出CK,PK,DN即可判断.
解:(1)由题意CD=CH,
在Rt△ACH中,CH=![]() =2
=2![]() ≈12.2(cm).
≈12.2(cm).
∴CD=CH=12.6(cm).
(2)如图2中,作EK⊥PC于K.
在Rt△ECK中,EK=ECsin53°≈4(cm),CK=ECcos53°≈3(cm),
在Rt△EPK中,PK=![]() =
=![]() =2
=2![]() ≈4.48(cm),
≈4.48(cm),
∴DP=CD﹣CK﹣PK﹣MN=12.6﹣3﹣4.48﹣2=3.12>2.5,
∴能在ND处装入一段长为2.5cm的订书钉.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
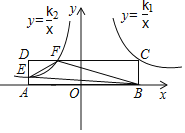
【题目】如图,矩形ABCD的顶点A,B在x轴上,且关于y轴对称,反比例函数y=![]() (x>0)的图象经过点C,反比例函数y=
(x>0)的图象经过点C,反比例函数y=![]() (x<0)的图象分别与AD,CD交于点E,F,若S△BEF=7,k1+3k2=0,则k1等于_____.
(x<0)的图象分别与AD,CD交于点E,F,若S△BEF=7,k1+3k2=0,则k1等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数 y kx b k 0的图象与反比例函数 y ![]() m 0的图象交于 A (-1,-1),B (n,2)两点.
m 0的图象交于 A (-1,-1),B (n,2)两点.
(1)求反比例函数和一次函数的表达式;
(2)点 P 在 x 轴上,过点 P 做垂直于 x 轴的直线 l,交直线 AB 于点 C,若AB=2AC,请直接写出点 C 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD 是菱形ABCD 的对角线,∠A=30°.
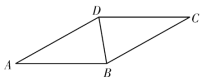
(1)请用尺规作图法,作AB 的垂直平分线EF,垂足为E,交AD 于F;(不要 求写作法,保留作图痕迹)
(2)在(1)的条件下,连接BF,求∠DBF 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=x+b与x轴、y轴分别交于A,B两点,与反比例函数y2=﹣![]() (x<0)的图象交于C,D两点,点C的横坐标为﹣1,过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.下列说法正确的是( )
(x<0)的图象交于C,D两点,点C的横坐标为﹣1,过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.下列说法正确的是( )
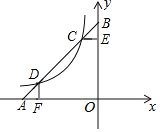
A.b=5
B.BC=AD
C.五边形CDFOE的面积为35
D.当x<﹣2时,y1>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.即:如图1,在Rt△ABC中,∠ACB=90°,∠ABC=30°,则:AC=![]() AB.
AB.

探究结论:小明同学对以上结论作了进一步研究.
(1)如图1,连接AB边上中线CE,由于CE=![]() AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
(2)如图2,点D是边CB上任意一点,连接AD,作等边△ADE,且点E在∠ACB的内部,连接BE.试探究线段BE与DE之间的数量关系,写出你的猜想并加以证明.
(3)当点D为边CB延长线上任意一点时,在(2)条件的基础上,线段BE与DE之间存在怎样的数量关系?请直接写出你的结论 .
拓展应用:如图3,在平面直角坐标系xOy中,点A的坐标为(﹣![]() ,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新能源汽车环保节能,越来越受到消费者的喜爱.各种品牌相继投放市场.一汽贸公司经销某品牌新能源汽车.去年销售总额为5000万元,今年1~5月份,每辆车的销售价格比去年降低1万元.销售数量与去年一整年的相同.销售总额比去年一整年的少20%,今年1~5月份每辆车的销售价格是多少万元?设今年1~5月份每辆车的销售价格为x万元.根据题意,列方程正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是线段
是线段![]() 上一点,
上一点,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作⊙
的长为半径作⊙![]() ,过点
,过点![]() 作
作![]() 的垂线交⊙
的垂线交⊙![]() 于
于![]() ,
,![]() 两点,点
两点,点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() 交⊙
交⊙![]() 于点
于点![]() ,以
,以![]() ,
,![]() 为边作
为边作![]() .
.
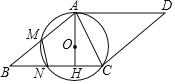
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,求四边形
,求四边形![]() 与⊙
与⊙![]() 重叠部分的面积;
重叠部分的面积;
(3)若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 和
和![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com