
【题目】如图,一次函数y=﹣x+4的图象与反比例![]() (k为常数,且k≠0)的图象交于A(1,a),B(b,1)两点,
(k为常数,且k≠0)的图象交于A(1,a),B(b,1)两点,

(1)求反比例函数的表达式及点A,B的坐标
(2)在x轴上找一点,使PA+PB的值最小,求满足条件的点P的坐标.
【答案】(1)A(1,3),B(3,1),反比例函数的表达式y=![]() ;(2)点P坐标(
;(2)点P坐标(![]() ,0).
,0).
【解析】
(1)把点A(1,a),B(b,1)代入一次函数y=﹣x+4,即可得出a,b,再把点A坐标代入反比例函数y=![]() ,即可得出结论;
,即可得出结论;
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB的值最小,求出直线AD的解析式,令y=0,即可得出点P坐标.
(1)把点A(1,a),B(b,1)代入一次函数y=﹣x+4,
得a=﹣1+4,1=﹣b+4,
解得a=3,b=3,
∴A(1,3),B(3,1);
点A(1,3)代入反比例函数y=![]() 得k=3,
得k=3,
∴反比例函数的表达式y=![]() ;
;
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB的值最小,
∴D(3,﹣1),
设直线AD的解析式为y=mx+n,
把A,D两点代入得,![]() ,
,
解得m=﹣2,n=5,
∴直线AD的解析式为y=﹣2x+5,
令y=0,得x=![]() ,
,
∴点P坐标(![]() ,0).
,0).



科目:初中数学 来源: 题型:
【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线C1:y=a1x2+b1x+c1和C2:y=a2x2+b2x+c2都经过原点,顶点分别为A,B,与x轴的另一个交点分别为M、N,如果点A与点B,点M与点N都关于原点O成中心对称,则抛物线C1和C2为姐妹抛物线,请你写出一对姐妹抛物线C1和C2,使四边形ANBM恰好是矩形,你所写的一对抛物线解析式是_______________________和_________________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E.
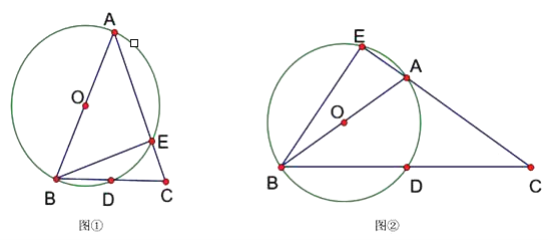
(1)当∠BAC为锐角时,如图①,求证:∠CBE=![]() ∠BAC;
∠BAC;
(2)当∠BAC为钝角时,如图②,CA的延长线与⊙O相交于点E,(1)中的结论是否仍然成立?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次“寻宝”人找到了如图所示的两个标志点A(2,3),B(4,1),A,B两点到“宝藏”点的距离都是![]() ,则“宝藏”点的坐标是( )
,则“宝藏”点的坐标是( )
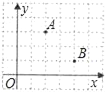
A. (1,0) B. (5,4) C. (1,0)或(5,4) D. (0,1)或(4,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,且当钟面显示3点30分时,分针垂直于桌面,A点距桌面的高度为10公分.如图2,若此钟面显示3点45分时,A点距桌面的高度为16公分,则钟面显示3点50分时,A点距桌面的高度为多少公分()
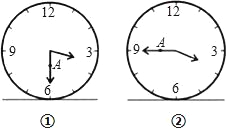
A. ![]() B. 16+π C. 18 D. 19
B. 16+π C. 18 D. 19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝祖国70周年华诞,阳光超市销售甲、乙两种庆祝商品,该超市若同时购进甲、乙两种商品各10件共花费400元;若购进甲种商品30件,购进乙种商品15件,将用去750元;
(1)求甲、乙两种商品每件的进价;
(2)由于甲、乙两种商品受到市民欢迎,十一月份超市决定购进甲、乙两种商品共80件,且保持(1)的进价不变,已知甲种商品每件的售价为15元,乙种商品每件的售价40元,要使十一月份购进的甲、乙两种商品共80件全部销售完的总利润不少于600元,那么该超市最多购进甲种商品多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com