
【题目】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.

科目:初中数学 来源: 题型:
【题目】(12分)如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).
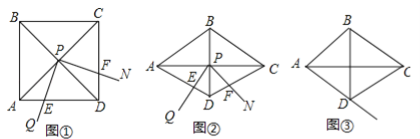
(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是 ;
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF=![]() AD,请给出证明;
AD,请给出证明;
(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是直角等腰△ABC斜边AB的中点,M为边AC上不和A、C重合的一动点,联结DM,过D作DNDM,交BC于N,联结MN.
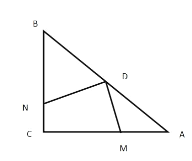
(1)求证:以AM、MN、BN为边的三角形是直角三角形
(2)如果AC2,AMx,试用x表示△DMN的面积,并求当ADM22.5时△DMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BC=8,点P由点B向点A运动,同时,点Q由点C出发沿线段AC的延长线运动,已知点P、Q运动速度相等,点Q与线段BC相交于点D,过点P作PE∥AQ,交BC于点E.
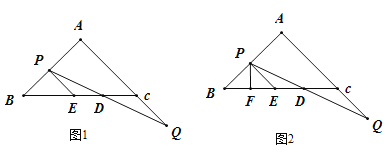
(1)如图1,求证:D为CE中点;
(2)如图2,过点P作PF⊥BC,垂足为点F,在P、Q的运动过程中,请判断DF的长度是否为定值;若是,请求出DF的长度;若否,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程
(1)2x2+4x﹣3=0(配方法解)
(2)5x2﹣8x+2=0(公式法解)
(3)3(x﹣5)2=2(5﹣x)
(4)(3x+2)(x+3)=x+14.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为调查本校学生固末平均每天做作业所用时间的情况,随机调查了50名同字,如图是根据调查所得数据绘制的统计图的一部分.请根据以上信息,解答下列问题
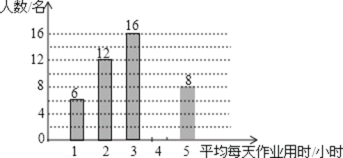
(1)请你补全条形统计图
(2)在这次调查的数据中,做作业所用时间的众数是 小时,中位数是 小时,平均数是 小时;
(3)若该校共有2000名学生,根据以上调查结果估计该校全体学生每天组作业时间在3小时内(含3小时)的同学共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
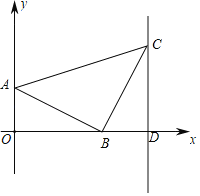
【题目】如图平面直角坐标系中,A点坐标为(0,1),AB=BC=![]() ,∠ABC=90°,CD⊥x轴.
,∠ABC=90°,CD⊥x轴.
(1)填空:B点坐标为 ,C点坐标为 .
(2)若点P是直线CD上第一象限上一点且△PAB的面积为6.5,求P点的坐标;
(3)在(2)的条件下点M是x轴上线段OD之间的一动点,当△PAM为等腰三角形时,直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
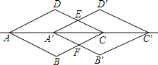
【题目】八年级数学学习合作小组在学过《图形的相似》这一章后,发现可将相似三角形的定义、判定以及性质拓展到矩形、菱形的相似中去.如:我们可以定义:“长和宽之比相等的矩形是相似矩形.”相似矩形也有以下的性质:相似矩形的对角线之比等于相似比,周长比等于相似比,面积比等于相似比的平方等等.请你参与这个学习小组,一同探索这类问题:
![]() 写出判定菱形相似的一种判定方法:若有一组角对应相等(或两组对角线对应成比例),则这两个菱形相似;
写出判定菱形相似的一种判定方法:若有一组角对应相等(或两组对角线对应成比例),则这两个菱形相似;
![]() 如图,将菱形
如图,将菱形![]() 沿着直线
沿着直线![]() 向右平移后得到菱形
向右平移后得到菱形![]() ,试证明:四边形
,试证明:四边形![]() 是菱形,且菱形
是菱形,且菱形![]() 菱形
菱形![]() ;
;
![]() 若
若![]() ,菱形
,菱形![]() 的面积是菱形
的面积是菱形![]() 面积的一半,求平移的距离
面积的一半,求平移的距离![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com