
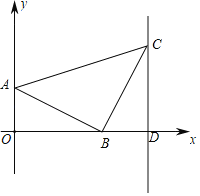
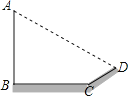
【题目】如图平面直角坐标系中,A点坐标为(0,1),AB=BC=![]() ,∠ABC=90°,CD⊥x轴.
,∠ABC=90°,CD⊥x轴.
(1)填空:B点坐标为 ,C点坐标为 .
(2)若点P是直线CD上第一象限上一点且△PAB的面积为6.5,求P点的坐标;
(3)在(2)的条件下点M是x轴上线段OD之间的一动点,当△PAM为等腰三角形时,直接写出点M的坐标.
【答案】(1)(3,0),(4,3);(2)P(4,4);(3)(1,0)或(![]() ).
).
【解析】
(1)根据勾股定理可求出OB=3,证明△AOB≌△DBC,可得出OA=BD=1,OB=DC=3,则B,C两点的坐标可求出;
(2)设P(4,a),由三角形面积可得出关于a的方程,解方程即可得出答案;
(3)根据M是x轴上线段OD之间的一动点,画出图形,有两种可能,当AP=MP或AM=MP时,设M(x,0),可得出关于x的方程,解方程即可得解.
解:(1)∵A点坐标为(0,1),AB=BC=![]() ,
,
∴OB=![]() =
=![]() =3,
=3,
∵∠ABC=90°,∠AOB=90°,
∴∠OAB+∠ABO=90°,∠ABO+∠CBD=90°,
∴∠OAB=∠CBD,
∵∠AOB=∠BDC,
∴△AOB≌△DBC(AAS),
∴OA=BD=1,OB=DC=3,
∴B(3,0),C(4,3),
故答案为:(3,0),(4,3);
(2)如图1,设P(4,a),
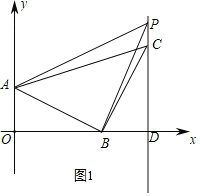
∵△PAB的面积为6.5,
∴S△PAB=S四边形AODP﹣S△AOB﹣S△BDP=![]() =6.5,
=6.5,
解得:a=4,
∴P(4,4);
(3)M是x轴上线段OD之间的一动点,如图2,当AP=MP,
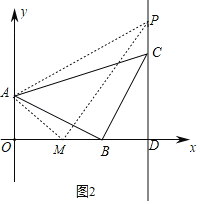
∵P(4,4),A(0,1),设M(x,0),
∴42+(4﹣1)2=(x﹣4)2+42,
解得:x1=1,x2=7(舍去),
∴M(1,0),
如图3,AM=MP时,
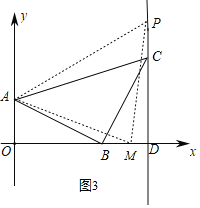
x2+12=(x﹣4)2+42,
解得x=![]() ,
,
∴![]() ,
,
综合以上可得点M的坐标为(1,0)或(![]() ).
).


科目:初中数学 来源: 题型:
【题目】某校八年级数学课外兴趣小组的同学积极参加义工活动,小庆对全体小组成员参加活动次数的情况进行统计解析,绘制了如下不完整的统计表和统计图(图).
次数 | 10 | 8 | 6 | 5 |
人数 | 3 | a | 2 | 1 |
(1)表中a= ;
(2)请将条形统计图补充完整;
(3)从小组成员中任选一人向学校汇报义工活动情况,参加了10次活动的成员被选中的概率有多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图③所示,图象过点(﹣1,0),对称轴为直线x=2,则下 列结论中正确的个数有( )
①4a+b=0;
②9a+3b+c<0;
③若点A(﹣3,y1),点B(﹣![]() ,y2),点C(5,y3)在该函数图象上,则y1<y3<y2;
,y2),点C(5,y3)在该函数图象上,则y1<y3<y2;
④若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 .
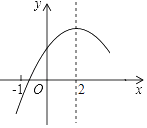
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,牧童家在B处,A、B两处相距河岸的距离AC、BD分别为500m和300m,且C、D两处的距离为600m,天黑牧童从A处将牛牵到河边去饮水,在赶回家,那么牧童最少要走( )
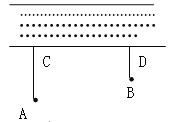
A.800mB.1000mC.1200mD.1500m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.
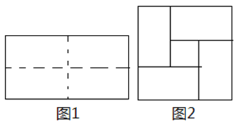
(1)选择题:图1是一个长2a、宽2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形.然后,按图2那样拼成一个(中间空的)正方形,则中间空的部分面积是( )
A.2ab B.(a+b)2 C.(a﹣b)2 D.a2﹣b2
(2)如图3,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积.据此,你能发现什么结论,请直接写出来:
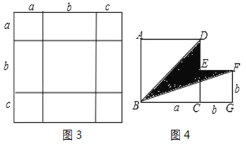
(3)如图4,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF.若两个正方形的边长满足a+b=10,ab=20,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为支援灾区建设,计划向![]() 、
、![]() 两受灾地运送急需物资分别为60吨和140吨,该市甲、乙两地有急需物资分别为120吨和80吨,已知甲、乙两地运到
两受灾地运送急需物资分别为60吨和140吨,该市甲、乙两地有急需物资分别为120吨和80吨,已知甲、乙两地运到![]() 、
、![]() 两地的每吨物资的运费如表所示:
两地的每吨物资的运费如表所示:
甲 | 乙 | |
| 20元/吨 | 15元/吨 |
| 25元/吨 | 24元/吨 |
(1)设甲地运到![]() 地的急需物资为
地的急需物资为![]() 吨,求总运费
吨,求总运费![]() (元)关于
(元)关于![]() (吨)的函数关系式,并写出
(吨)的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)求最低总运费,并说明总运费最低时的运送方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某天小明发现阳光下电线杆AB的影子落在土坡的坡面CD和地面BC上,量的CD=8米,BC=20米,斜坡CD的坡度比为1:![]() ,且此时测得1米杆的影长为2米,则电线杆的高度为( )
,且此时测得1米杆的影长为2米,则电线杆的高度为( )
A.(14+2![]() )米 B.28米 C.(7+
)米 B.28米 C.(7+![]() )米 D.9米
)米 D.9米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com