
【题目】如图,点D是直角等腰△ABC斜边AB的中点,M为边AC上不和A、C重合的一动点,联结DM,过D作DNDM,交BC于N,联结MN.
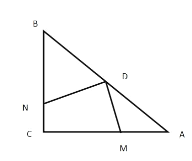
(1)求证:以AM、MN、BN为边的三角形是直角三角形
(2)如果AC2,AMx,试用x表示△DMN的面积,并求当ADM22.5时△DMN的面积.
【答案】(1)见解析;(2)![]() ,
,![]()
【解析】
(1)连接![]() 、MN,结合等腰直角三角形的性质利用ASA可证
、MN,结合等腰直角三角形的性质利用ASA可证![]() ,由全等三角形的性质可得
,由全等三角形的性质可得![]() ,
,![]() ,由
,由![]() 是直角三角形可知以
是直角三角形可知以![]() 为边的三角形时直角三角形;
为边的三角形时直角三角形;
(2)易知![]() ,
,![]() ,由勾股定理可得MN长,由(1)中
,由勾股定理可得MN长,由(1)中![]() 可知
可知![]() ,结合勾股定理可知MD长,根据三角形面积公式可用x表示出△DMN的面积,当ADM22.5时,可得
,结合勾股定理可知MD长,根据三角形面积公式可用x表示出△DMN的面积,当ADM22.5时,可得![]() ,在
,在![]() 中,根据勾股定理可得CD长,求出x值代入△DMN的面积的表达式中即可求解.
中,根据勾股定理可得CD长,求出x值代入△DMN的面积的表达式中即可求解.
(1) 如图,连接![]() 、MN,
、MN,
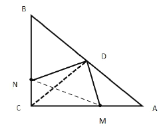
![]() 是等腰直角三角形
是等腰直角三角形
![]()
![]() 点D是AB的中点
点D是AB的中点
![]()
![]()
![]()
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,
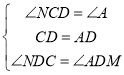
![]()
∴![]()
![]()
![]()
![]() 是直角三角形,即以
是直角三角形,即以![]() 为边的三角形时直角三角形
为边的三角形时直角三角形
∴以![]() 为边的三角形时直角三角形
为边的三角形时直角三角形
(2)![]() ,由(1)知
,由(1)知![]()
在![]() 中,根据勾股定理得
中,根据勾股定理得![]() ,
,
![]()
![]()
在![]() 中,根据勾股定理得
中,根据勾股定理得![]()
即 ![]() ,
,![]()
所以![]()
当![]() 时,
时,![]() ,
,
![]()
![]()
![]() ,
,
在![]() 中,根据勾股定理得
中,根据勾股定理得![]()
由(1)知![]()
![]() ,
,![]()
![]() ,解得
,解得![]()
将![]() 代入
代入![]() 得
得![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,![]() 是边长为9的等边三角形,
是边长为9的等边三角形,![]() 是
是![]() 边上一动点,由
边上一动点,由![]() 向
向![]() 运动(与
运动(与![]() 、
、![]() 不重合),
不重合),![]() 是
是![]() 延长线上一动点,与点
延长线上一动点,与点![]() 同时以相同的速度由
同时以相同的速度由![]() 向
向![]() 延长线方向运动(
延长线方向运动(![]() 不与
不与![]() 重合),过
重合),过![]() 作
作![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]()

(1)若![]() 时,求
时,求![]() 的长
的长
(2)当点![]() ,
,![]() 运动时,线段
运动时,线段![]() 与线段
与线段![]() 是否相等?请说明理由
是否相等?请说明理由
(3)在运动过程中线段![]() 的长是否发生变化?如果不变,求出线段
的长是否发生变化?如果不变,求出线段![]() 的长;如果发生变化,请说明理由
的长;如果发生变化,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在东西方向的海岸线MN上有A,B两港口,海上有一座小岛P,渔民每天都乘轮船从A,B 两港口沿AP,BP的路线去小岛捕鱼作业.已知小岛P在A港的北偏东60°方向,在B港的北偏西45°方向,小岛P距海岸线MN的距离为30海里.
(1)求AP,BP的长(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7,
≈1.7,![]() ≈2.2);
≈2.2);
(2)甲、乙两船分别从A,B两港口同时出发去小岛P捕鱼作业,甲船比乙船晚到小岛24分钟.已知甲船速度是乙船速度的1.2倍,利用(1)中的结果求甲、乙两船的速度各是多少海里/时?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级数学课外兴趣小组的同学积极参加义工活动,小庆对全体小组成员参加活动次数的情况进行统计解析,绘制了如下不完整的统计表和统计图(图).
次数 | 10 | 8 | 6 | 5 |
人数 | 3 | a | 2 | 1 |
(1)表中a= ;
(2)请将条形统计图补充完整;
(3)从小组成员中任选一人向学校汇报义工活动情况,参加了10次活动的成员被选中的概率有多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(2,8),且与x轴相切于点B.
(1)当x>0,y=5时,求x的值;
(2)当x = 6时,求⊙P的半径;
(3)求y关于x的函数表达式,请判断此函数图象的形状,并在图②中画出此函数的图象(不必列表,画草图即可).


图① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-1,4),B(-5,3),C(-3,2).
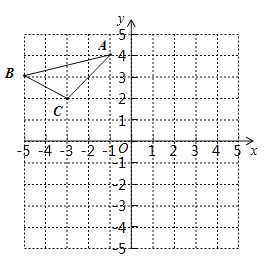
(1)将△ABC向下平移6个单位后得到△A1B1C1,请在图中画出△A1B1C1,并写出C1点坐标;
(2)图中点A2(1,2)与点A关于直线l成轴对称,请在图中画出直线l及△ABC关于直线l对称的△A2B2C2,并写出B2点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为支援灾区建设,计划向![]() 、
、![]() 两受灾地运送急需物资分别为60吨和140吨,该市甲、乙两地有急需物资分别为120吨和80吨,已知甲、乙两地运到
两受灾地运送急需物资分别为60吨和140吨,该市甲、乙两地有急需物资分别为120吨和80吨,已知甲、乙两地运到![]() 、
、![]() 两地的每吨物资的运费如表所示:
两地的每吨物资的运费如表所示:
甲 | 乙 | |
| 20元/吨 | 15元/吨 |
| 25元/吨 | 24元/吨 |
(1)设甲地运到![]() 地的急需物资为
地的急需物资为![]() 吨,求总运费
吨,求总运费![]() (元)关于
(元)关于![]() (吨)的函数关系式,并写出
(吨)的函数关系式,并写出![]() 的取值范围;
的取值范围;
(2)求最低总运费,并说明总运费最低时的运送方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com