
【题目】如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(2,8),且与x轴相切于点B.
(1)当x>0,y=5时,求x的值;
(2)当x = 6时,求⊙P的半径;
(3)求y关于x的函数表达式,请判断此函数图象的形状,并在图②中画出此函数的图象(不必列表,画草图即可).


图① 图②
【答案】(1)x=6;(2)y=5,则圆P的半径为5;(3)图象为抛物线,图象见解析
【解析】
(1)由y=5,得到P(x,5),连接AP,PB,由切线的性质知PB⊥x轴,结合勾股定理可求出x的值;
(2)由题意得到AP=PB,根据勾股定理求出y的值,即为圆P的半径;
(3)把(2)中得到的式子![]() =y整理,确定出y关于x的函数解析式,画出函数图象即可;
=y整理,确定出y关于x的函数解析式,画出函数图象即可;
解:(1)由y=5,得到P(x,5),连接AP,PB,
∵圆P与x轴相切,
∴PB⊥x轴,
即PB=5,
由AP=PB,由勾股定理得,x=2+![]() =2+4=6,
=2+4=6,
∴x=6.
(2)由x=6,得到P(6,y),连接AP,PB,
∵圆P与x轴相切,
∴PB⊥x轴,即PB=y,由AP=PB,得到![]() =y,
=y,
解得:y=5,则圆P的半径为5;
(3)同(2),由AP=PB,得到(x﹣2)2+(8﹣y)2=y2,
整理得:![]() =
=![]() ,
,
即图象为抛物线,
画出函数图象,如图②所示;


科目:初中数学 来源: 题型:
【题目】中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书“,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本书最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表,如图所示:
本数(本) | 频数(人数) | 频率 |
5 | a | 0.2 |
6 | 18 | 0.36 |
7 | 14 | b |
8 | 8 | 0.16 |
合计 | 50 | c |
我们定义频率=![]() ,比如由表中我们可以知道在这次随机调查中抽样人数为50人课外阅读量为6本的同学为18人,因此这个人数对应的频率就是
,比如由表中我们可以知道在这次随机调查中抽样人数为50人课外阅读量为6本的同学为18人,因此这个人数对应的频率就是![]() =0.36.
=0.36.
(1)统计表中的a、b、c的值;
(2)请将频数分布表直方图补充完整;
(3)求所有被调查学生课外阅读的平均本数;
(4)若该校八年级共有600名学生,你认为根据以上调查结果可以估算分析该校八年级学生课外阅读量为7本和8本的总人数为多少吗?请写出你的计算过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,
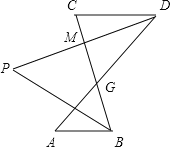
(1)如图,![]() ,
,![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 的平分线,求
的平分线,求![]() 的度数;
的度数;
(2)如果(1)中条件变为![]() ,
,![]() ,其它条件不变,则
,其它条件不变,则![]() _____________.(直接写出答案)
_____________.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直径为1000毫米的圆柱形油罐内装进一些油.其横截面如图.油面宽AB=600毫米.
(1)求油的最大深度;
(2)如果再注入一些油后,油面宽变为800毫米,此时油面上升了多少毫米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是直角等腰△ABC斜边AB的中点,M为边AC上不和A、C重合的一动点,联结DM,过D作DNDM,交BC于N,联结MN.
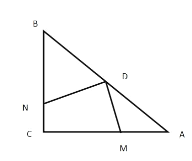
(1)求证:以AM、MN、BN为边的三角形是直角三角形
(2)如果AC2,AMx,试用x表示△DMN的面积,并求当ADM22.5时△DMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程
(1)2x2+4x﹣3=0(配方法解)
(2)5x2﹣8x+2=0(公式法解)
(3)3(x﹣5)2=2(5﹣x)
(4)(3x+2)(x+3)=x+14.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D在△ABC内,BD=BC,∠DBC=60°,点E在△ABC外,∠BCE=150°,∠ABE=60°.
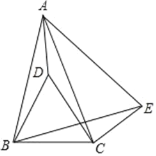
(1)求证:△ADB≌△ADC , 并求出∠ADB的度数;
(2)小明说△ABE是等腰三角形,小华说△ABE是等边三角形.请问 说法更准确,并说明理由.
(3)连接DE,若DE⊥BD,DE=8,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com