
【题目】在直径为1000毫米的圆柱形油罐内装进一些油.其横截面如图.油面宽AB=600毫米.
(1)求油的最大深度;
(2)如果再注入一些油后,油面宽变为800毫米,此时油面上升了多少毫米?

【答案】(1)100mm;(2)此时油面上升了100毫米或700毫米
【解析】
(1)作OF⊥AB交AB于F,交圆于G,连接OA,由垂径定理可求AF=300 mm,再由勾股定理求出OF的长,即可求出水深GF的长;
(2)连接OC,分水面在圆心下方和圆心上方两种情况求解即可.
解:(1)作OF⊥AB交AB于F,交圆于G,连接OA,
∴AF=![]() AB=300 mm,由勾股定理得,OF=
AB=300 mm,由勾股定理得,OF=![]() =400 mm,
=400 mm,
则GF=OG﹣OF=100mm;
(2)连接OC,
∵OE⊥CD,
∴CE=400 mm,OE=![]() =300 mm,
=300 mm,
则EF=OG﹣OE﹣FG=100 mm,
同理,当CD在圆心O上方时,可得EF=700 mm.
答:此时油面上升了100毫米或700毫米.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
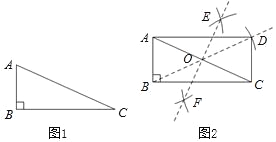
【题目】下面是“利用直角三角形作矩形”尺规作图的过程.
已知:如图1,在Rt△ABC中,∠ABC=90°.
求作:矩形ABCD.
小明的作法如下:
如图2,(1)分别以点A、C为圆心,大于![]() AC同样长为半径作弧,两弧交于点E、F;
AC同样长为半径作弧,两弧交于点E、F;
(2)作直线EF,直线EF交AC于点O;
(3)作射线BO,在BO上截取OD,使得OD=OB;
(4)连接AD,CD.
∴四边形ABCD就是所求作的矩形.
老师说,“小明的作法正确.”
请回答,小明作图的依据是:__________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 与x轴交于E(-2,0),与y轴交于点A.
与x轴交于E(-2,0),与y轴交于点A.![]() 与x轴交于B(2,0),与y轴交于点D(0,-4).它们的图象如图所示,请依据图象回答以下问题:
与x轴交于B(2,0),与y轴交于点D(0,-4).它们的图象如图所示,请依据图象回答以下问题:
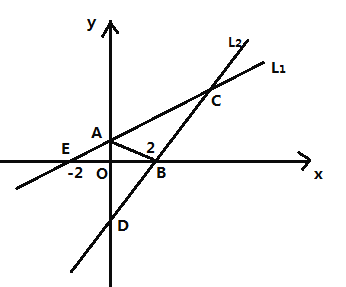
(1)a=
(2)确定![]() 的函数关系式
的函数关系式
(3)求△ABC的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
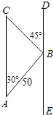
【题目】一架外国侦察机沿![]() 方向侵入我国领空进行非法侦察,我空军的战斗机沿
方向侵入我国领空进行非法侦察,我空军的战斗机沿![]() 方向与外国侦察机平行飞行,进行跟踪监视,我机在
方向与外国侦察机平行飞行,进行跟踪监视,我机在![]() 处与外国侦察机
处与外国侦察机![]() 处的距离为
处的距离为![]() 米,
米,![]() 为
为![]() ,这时外国侦察机突然转向,以偏左
,这时外国侦察机突然转向,以偏左![]() 的方向飞行,我机继续沿
的方向飞行,我机继续沿![]() 方向以
方向以![]() 米/秒的速度飞行,外国侦察机在
米/秒的速度飞行,外国侦察机在![]() 点故意撞击我战斗机,使我战斗机受损.问外国侦察机由
点故意撞击我战斗机,使我战斗机受损.问外国侦察机由![]() 到
到![]() 的速度是多少?(结果保留整数,参考数据
的速度是多少?(结果保留整数,参考数据![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(2,8),且与x轴相切于点B.
(1)当x>0,y=5时,求x的值;
(2)当x = 6时,求⊙P的半径;
(3)求y关于x的函数表达式,请判断此函数图象的形状,并在图②中画出此函数的图象(不必列表,画草图即可).


图① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC≌Rt△CED,点B、C、E在同一直线上,则结论:①AC=CD,②AC⊥CD,③BE=AB+DE,④AB∥ED,其中成立的有( )

A. 仅① B. 仅①③ C. 仅①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠C=90°,点O是AB的中点,边AC的长为6,将一块边长足够长的三角板的直角顶点放在O点处,将三角板绕着点O旋转,始终保持三角板的直角边与AC相交,交点为点D,另一条直角边与BC相交,交点为点E,则等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为( )
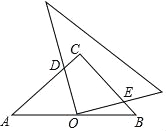
A. 7 B. 6 C. 5 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
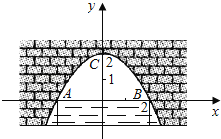
【题目】图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,建立如图所示的平面直角坐标系:
(1)求拱桥所在抛物线的解析式;
(2)当水面下降1m时,则水面的宽度为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com