
【题目】如图,菱形ABCD的对角线交于点O,DF∥AC,CF∥BD.

(1)求证:四边形OCFD是矩形;(2)若AD=5,BD=8,计算tan∠DCF的值.
【答案】(1)见解析;(2)tan∠DCF=![]() .
.
【解析】
(1)根据已知条件得到四边形OCFD是平行四边形,根据菱形的性质得到∠DOC=90°,即可得到结论;
(2)根据菱形的性质得到AD=CD,得到CD=5,OD=OB=![]() BD,求得OD=4,根据矩形的性质得到OD=CF,解直角三角形即可得到结论.
BD,求得OD=4,根据矩形的性质得到OD=CF,解直角三角形即可得到结论.
(1)证明:∵DF∥AC,CF∥BD,
∴四边形OCFD是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠DOC=90°,
∴平行四边形OCFD是矩形;
(2)解:∵四边形ABCD是菱形,
∴AD=CD,
∵AD=5,
∴CD=5,
∵菱形ABCD两条对角线交于O,
∴OD=OB=![]() BD,
BD,
∴OD=4,
∵四边形OCFD是矩形,
∴OD=CF,
∴在Rt△CFD中,CF2+DF2=CD2,
∴DF=3,
∴tan∠DCF=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】为迎接“世界华人炎帝故里寻根节”,某工厂接到一批纪念品生产订单,按要求在15天内完成,约定这批纪念品的出厂价为每件20元,设第x天(1≤x≤15,且x为整数)每件产品的成本是p元,p与x之间符合一次函数关系,部分数据如表:
天数(x) | 1 | 3 | 6 | 10 |
每件成本p(元) | 7.5 | 8.5 | 10 | 12 |
任务完成后,统计发现工人李师傅第x天生产的产品件数y(件)与x(天)满足如下关系:y=![]() ,
,
设李师傅第x天创造的产品利润为W元.
(1)直接写出p与x,W与x之间的函数关系式,并注明自变量x的取值范围:
(2)求李师傅第几天创造的利润最大?最大利润是多少元?
(3)任务完成后.统计发现平均每个工人每天创造的利润为299元.工厂制定如下奖励制度:如果一个工人某天创造的利润超过该平均值,则该工人当天可获得20元奖金.请计算李师傅共可获得多少元奖金?
查看答案和解析>>
科目:初中数学 来源: 题型:
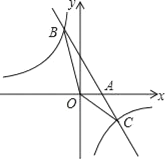
【题目】如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=![]() 相交于B(﹣1,5),C(
相交于B(﹣1,5),C(![]() ,d)两点.
,d)两点.
(1)利用图中条件,求反比例和一次函数的解析式;
(2)连接OB,OC,求△BOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E分别为△ABC的边AB、AC上的点,BE与CD相交于点O,现有四个条件:①AB=AC;②OB=OC;③∠ABE=∠ACD;④BE=CD,选择其中2个条件作为题设,余下2个条件作为结论,所有命题中,真命题的个数为( )
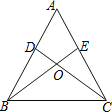
A. .3B. .4C. .5D. 、6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考体育测评前,某校在初三15个班中随机抽取了4个班的学生进行了摸底测评,将各班的满分人数进行整理,绘制成如下两幅统计图.
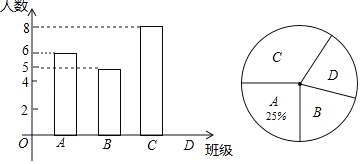
(1)D班满分人数共 人,扇形统计图中,表示C班满分人数的扇形圆心角的度数为 .
(2)这些满分同学中有4名同学(3女1男)的跳绳动作十分标准,学校准备从这4名同学中任选2名同学作示范,请利用画树状图或列表法求选中1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(0,2),B(2,2),抛物线F:y=x2﹣2mx+m2﹣2.

(1)求抛物线F的顶点坐标(用含m的式子表示);
(2)当抛物线F与线段AB有公共点时,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
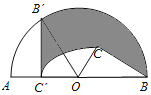
【题目】如图,C为半圆内一点,O为圆心,直径AB长为2cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为_____cm2.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.
(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完,其中每辆大货车一次运费花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,举行抽奖活动,并规定:顾客每购买100元的商品,就可随机抽取一张奖劵,抽得奖券“紫气东来”、“花开富贵”、“吉星高照”,就可以分别获得100元、50元、20元的购物券,抽得“谢谢惠顾”不赠购物券;如果顾客不愿意抽奖,可以直接获得购物券10元.小明购买了100元的商品,他看到商场公布的前10000张奖券的抽奖结果如下:

(1)求“紫气东来”奖券出现的频率;
(2)请你帮助小明判断,抽奖和直接获得购物券,哪种方式更合算?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com