
【题目】中考体育测评前,某校在初三15个班中随机抽取了4个班的学生进行了摸底测评,将各班的满分人数进行整理,绘制成如下两幅统计图.
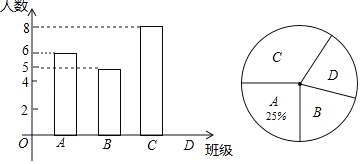
(1)D班满分人数共 人,扇形统计图中,表示C班满分人数的扇形圆心角的度数为 .
(2)这些满分同学中有4名同学(3女1男)的跳绳动作十分标准,学校准备从这4名同学中任选2名同学作示范,请利用画树状图或列表法求选中1男1女的概率.
【答案】(1)5,120°;(2)见解析,![]() .
.
【解析】
(1)由A的人数和其所占的百分比即可求出总人数,由此即可求出D班满分人数,根据C班满分人数的百分比可求出其所对应扇形的圆心角的度数;
(2)列表得出所有等可能的情况数,找出刚好抽到一男一女的情况数,即可求出所求的概率.
解:(1)满分人数为6÷25%=24(人),
∴D班满分人数共24﹣6﹣5﹣8=5(人),
C班满分人数的扇形圆心角的度数=360°×![]() =120°,
=120°,
故答案为:5;120°;
(2)画树状图为:

或列表如下:
男 | 女1 | 女2 | 女3 | |
男 | ﹣﹣﹣ | (女,男) | (女,男) | (女,男) |
女1 | (男,女) | ﹣﹣﹣ | (女,女) | (女,女) |
女2 | (男,女) | (女,女) | ﹣﹣﹣ | (女,女) |
女3 | (男,女) | (女,女) | (女,女) | ﹣﹣﹣ |
∵共有12种等可能情况,1男1女有6种情况,设题中1男1女为事件A,
∴P(A)=![]() =
=![]() .
.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】某地要改造部分农田种植蔬菜.经调查,平均每亩改造费用是![]() 元,添加滴灌设备等费用(元)与改造面积
元,添加滴灌设备等费用(元)与改造面积![]() (亩)的平分成正比,比例系数为
(亩)的平分成正比,比例系数为![]() ,以上两项费用
,以上两项费用![]() 年内不需要增加;每亩种植蔬菜还需种子、人工费用
年内不需要增加;每亩种植蔬菜还需种子、人工费用![]() 元,这项费用每年均需开支.设改造
元,这项费用每年均需开支.设改造![]() 亩,每亩蔬菜年均销售金额为
亩,每亩蔬菜年均销售金额为![]() 元,除上述费用外,没有其他费用.
元,除上述费用外,没有其他费用.
(1)设当年收益为![]() 元,求
元,求![]() 与
与![]() 的函数关系式(用含
的函数关系式(用含![]() 的式子表示);
的式子表示);
(2)若![]() ,如果按
,如果按![]() 年计算,是否改造面积越大收益越大?改造面积为多少时可以得到最大收益?
年计算,是否改造面积越大收益越大?改造面积为多少时可以得到最大收益?
(3)若![]() 时,按
时,按![]() 年计算,能确保改造的面积越大收益也越大,求
年计算,能确保改造的面积越大收益也越大,求![]() 的取值范围.
的取值范围.
注:收益=销售金额-(改造费+滴灌设备等费+种子、人工费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
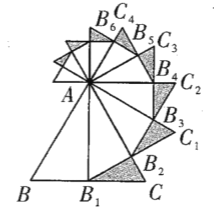
【题目】如图,已知等边![]() 的边长是
的边长是![]() ,以
,以![]() 边上的高
边上的高![]() ,为边作等边三角形,得到第一个等边
,为边作等边三角形,得到第一个等边![]() ;再以等边
;再以等边![]() 的
的![]() 边上的高
边上的高![]() ,为边作等边三角形,得到第二个等边
,为边作等边三角形,得到第二个等边![]() ,再以等边
,再以等边![]() 的
的![]() 边上的高
边上的高![]() 为边作等边三角形,得到第三个等边
为边作等边三角形,得到第三个等边![]() : ....记
: ....记![]() 的面积为
的面积为![]() 的面积为
的面积为![]() 的面积为
的面积为![]() ,如此下去,则
,如此下去,则![]() ___________
___________
查看答案和解析>>
科目:初中数学 来源: 题型:
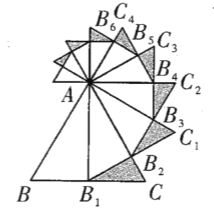
【题目】如图,已知等边![]() 的边长是
的边长是![]() ,以
,以![]() 边上的高
边上的高![]() ,为边作等边三角形,得到第一个等边
,为边作等边三角形,得到第一个等边![]() ;再以等边
;再以等边![]() 的
的![]() 边上的高
边上的高![]() ,为边作等边三角形,得到第二个等边
,为边作等边三角形,得到第二个等边![]() ,再以等边
,再以等边![]() 的
的![]() 边上的高
边上的高![]() 为边作等边三角形,得到第三个等边
为边作等边三角形,得到第三个等边![]() : ....记
: ....记![]() 的面积为
的面积为![]() 的面积为
的面积为![]() 的面积为
的面积为![]() ,如此下去,则
,如此下去,则![]() ___________
___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为4、中心为![]() 的正方形
的正方形![]() 如图所示,动点
如图所示,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒1个单位长度的速度运动到点
以每秒1个单位长度的速度运动到点![]() 时停止,动点
时停止,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒2个单位长度的速度运动一周停止,若点
以每秒2个单位长度的速度运动一周停止,若点![]() 同时开始运动,点
同时开始运动,点![]() 的运动时间为
的运动时间为![]()
![]() ,当
,当![]() 时,满足
时,满足![]() 的点
的点![]() 的位置有( )
的位置有( )

A.6个B.7个C.8个D.9个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com