
【题目】已知二次函数![]() (
(![]() 为常数),当
为常数),当![]() 时,函数的最小值为5,则
时,函数的最小值为5,则![]() 的值为( )
的值为( )
A.-1或5B.-1或3C.1或5D.1或3
【答案】A
【解析】
由解析式可知该函数在x=h时取得最小值1,x>h时,y随x的增大而增大;当x<h时,y随x的增大而减小;根据1≤x≤3时,函数的最小值为5可分如下两种情况:①若h<1,可得x=1时,y取得最小值5;②若h>3,可得当x=3时,y取得最小值5,分别列出关于h的方程求解即可.
解:∵x>h时,y随x的增大而增大,当x<h时,y随x的增大而减小,
∴①若h<1,当![]() 时,y随x的增大而增大,
时,y随x的增大而增大,
∴当x=1时,y取得最小值5,
可得:![]() ,
,
解得:h=1或h=3(舍),
∴h=1;
②若h>3,当![]() 时,y随x的增大而减小,
时,y随x的增大而减小,
当x=3时,y取得最小值5,
可得:![]() ,
,
解得:h=5或h=1(舍),
∴h=5,
③若1≤h≤3时,当x=h时,y取得最小值为1,不是5,
∴此种情况不符合题意,舍去.
综上所述,h的值为1或5,
故选:A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】解决问题.
学校要购买A,B两种型号的足球,按体育器材门市足球销售价格(单价)计算:若买2个A型足球和3个B型足球,则要花费370元,若买3个A型足球和1个B型足球,则要花费240元.
(1)求A,B两种型号足球的销售价格各是多少元/个?
(2)学校拟向该体育器材门市购买A,B两种型号的足球共20个,且费用不低于1300元,不超过1500元,则有哪几种购球方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果品超市经销一种水果,已知该水果的进价为每千克15元,通过一段时间的销售情况发现,该种水果每周的销售总额相同,且每周的销售量![]() (千克)与每千克售价
(千克)与每千克售价![]() (元)的关系如表所示:
(元)的关系如表所示:
每千克售价 | 25 | 30 | 40 |
每周销售量 | 240 | 200 | 150 |
(1)求出每周销售量![]() (千克)与每千克售价
(千克)与每千克售价![]() (元)的函数关系式.
(元)的函数关系式.
(2)由于销售淡季即将来临,超市要完成每周销售量不低于300千克的任务,则该种水果每千克售价最多定为多少元?
(3)在(2)的基础上,超市销售该种水果能否达到每周获利2000元?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】改革开放40年以来,城乡居民生活水平持续快速提升.居民教育、文化和娱乐消费支出持续增长,已经成为居民各项消费支出中仅次于居住、食品烟酒、交通通信后的第四大消费支出.下图为北京市统计局发布的2017年和2018年我市居民人均教育、文化和娱乐消费支出的折线图:
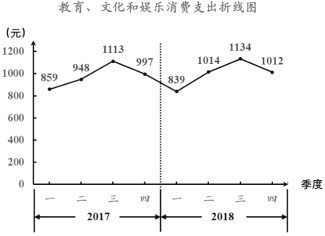
说明:在统计学中,同比是指本期统计数据与上一年同期统计数据相比较,例如2018年第二季度与2017年第二季度相比较;环比是指本期统计数据与上期统计数据相比较,例如2018年第二季度与2018年第一季度相比较.
根据上述信息,下列结论中错误的是( ).
A.2017年第二季度环比有所提高B.2017年第四季度环比有所下降
C.2018年第一季度同比有所提高D.2017和2018年支出最高的都是第三季度
查看答案和解析>>
科目:初中数学 来源: 题型:
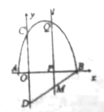
【题目】如图,在Rt△ABC中,∠C = 90°,点O是斜边AB上一定点,到点O的距离等于OB的所有点组成图形W,图形W与AB,BC分别交于点D,E,连接AE,DE,∠AED=∠B.

(1)判断图形W与AE所在直线的公共点个数,并证明.
(2)若![]() ,
,![]() ,求OB.
,求OB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表,是池州市今年“五一”这周内日最高气温的统计表,关于这7天的日最高气温的众数,中位数,方差分别是:( )
日期 | 29日 | 30日 | 5月1日 | 2日 | 3日 | 4日 | 5日 |
日最高气温 | 16°C | 19°C | 22°C | 24°C | 26°C | 24°C | 23°C |
A. 24,23,10B. 24,23,![]() C. 24,22,10D. 24,22,
C. 24,22,10D. 24,22,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考体育测评前,某校在初三15个班中随机抽取了4个班的学生进行了摸底测评,将各班的满分人数进行整理,绘制成如下两幅统计图.
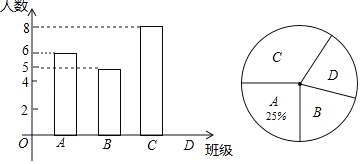
(1)D班满分人数共 人,扇形统计图中,表示C班满分人数的扇形圆心角的度数为 .
(2)这些满分同学中有4名同学(3女1男)的跳绳动作十分标准,学校准备从这4名同学中任选2名同学作示范,请利用画树状图或列表法求选中1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交抛物线于点
交抛物线于点![]() .
.
(1)求点![]() 、点
、点![]() 、点
、点![]() 的坐标;
的坐标;
(2)当点![]() 在线段
在线段![]() 上运动时,直线
上运动时,直线![]() 交
交![]() 于点
于点![]() ,试探究当
,试探究当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形;
是平行四边形;
(3)在点![]() 的运动过程中,是否存在点
的运动过程中,是否存在点![]() ,使
,使![]() 是以
是以![]() 为直角边的直角三角形?若存在,求出点
为直角边的直角三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com